Силы инерции

Рассмотрим теперь вопрос о том, как формулируются законы механики

в неинерциальных системах отсчета. Вопрос этот имеет важное практическое значение: система отсчета, связанная с поверхностью Земли, не является инерциальной — например, в системе отсчета, связанной с Солнцем, точки на поверхности Земли испытывают центростремительное ускорение, обусловленное вращением Земли вокруг собственной оси и вокруг Солнца.

При определенных условиях этой неинерциальностью можно пренебречь, но при решении многих практических задач (например, запуск космического корабля) без учета этой неинерциальности не обойтись. К тому же, многие машины и механизмы реально работают в неинерциальных системах отсчета — в движущихся с ускорением вагонах, самолетах, космических кораблях и так далее.

Итак, посмотрим, как преобразуется основной закон механики — второй

закон Ньютона — при переходе от инерциальной системы отсчета к неинерциальной. Остановимся отдельно на двух случаях: рассмотрим сначала простейший случай поступательного движения неинерциальной системы, а затем обсудим, как видоизменяются законы механики во вращающейся системе отсчета.

Поступательное движение неинерциальной системы отсчета. В повседневной жизни каждому из нас чуть ли не ежедневно приходится испытывать неприятные ощущения, когда при резком торможении автобуса или вагона метро какая-то сила бросает нас вперед. Чтобы понять происхождение этой силы, рассмотрим две системы отсчета: инерциальную систему К и систему К', которая совершает поступательное движение относительно системы К с ускорением А, зависящем в общем случае от времени

(рис. 9.2). Пусть r и r' — радиусы-векторы материальной точки с массой

m в инерциальной и неинерциальной системах, соответственно, a R(t)

радиус-вектор начала отсчета системы К' относительно системы К.

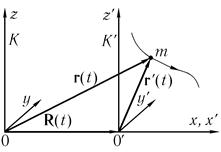
Рис. 9.2

Уравнение движения материальной точки в инерциальной системе отсчета

К — второй закон Ньютона:

m a = F,

где F — результирующая сила, действующая на рассматриваемую материальную точку со стороны других тел,

а = d² r /dt² — ускорение материальной точки в инерциальной системе. Координаты и скорости материальной точки в системах К и К' связаны друг с другом соотношениями (9.1), (9.2).

Если тело неподвижно относительно К', то движение этой системы приводит к переносу тела относительно К. Скорость V называется переносной скоростью. Скорость относительно системы К', т. е. v' так и называется — относительная скорость. Наконец, скорость v в инерциальной системе К носит название абсолютной скорости. Надо понимать условность последнего названия: это, конечно, просто скорость относительно системы К. Но К — система инерциальная, в некоторой степени «привилегированная», и

только в этом условном смысле скорость может быть названа абсолютной.

Продифференцировав еще раз по времени обе части равенства (9.2), получаем соотношение между ускорениями

а = А + а '. (9.4)

Здесь, соответственно, а — абсолютное ускорение, А — переносное и а ' —

относительное. Подставив полученное выражение для а во второй закон

Ньютона, перепишем его в виде

m a ' = F - m A. (9.5)

Как мы видим, уравнение движения в неинерциальной системе отсчета (9.5) отличается от второго закона Ньютона в инерциальной системе (9.2) тем, что в правой части уравнения наряду с силой F появляется еще добавочное слагаемое -mA. Если ввести обозначение

-m A = F_in, (9.6)

то уравнение движения в неинерциальной системе примет такой же привычный вид, как и второй закон Ньютона,

m a ' = F + F_in, (9.7)

где определенное равенством (9.6) добавочное слагаемое F_ин называют силой

инерции, конкретно — поступательной силой инерции. Далее мы познакомимся и с другими силами инерции.

В данном случае сила инерции является пространственно-однородной,

т. е. сила инерции при поступательном движении неинерциальной системы отсчета имеет одно и тоже значение для всех точек этой системы. Это следует из (9.6): сила инерции зависит только от ускорения, с которым начало неинерциальной системы К' движется относительно инерциальной системы К.

Итак, движение относительно рассматриваемой неинерциальной системы можно исследовать двумя способами. Можно определить закон движения материальной точки r (t) в некоторой инерциальной системе, используя второй закон Ньютона в его стандартном виде, а затем пересчитать его относительно неинерциальной системы, т. е. получить y' (t) из закона преобразования координат (9.1) (при условии, конечно, что закон движения неинерциальной системы R (t) известен). Но можно сразу решать задачу в

неинерциальной системе отсчета с помощью видоизмененного второго закона Ньютона (9.7), в котором в правой части к реальной силе F, определяемой

взаимодействием рассматриваемого тела с другими телами, добавлена сила инерции F_in, определяемая соотношением (9.6). Появление этой добавочной силы при рассмотрении движения относительно неинерциальной системы отсчета — формальное следствие преобразования координат (8.7) и не отражает появления какого-либо нового воздействия на материальную точку со стороны других тел. В этом смысле силу инерции можно назвать фиктивной силой, хотя для наблюдателя в неинерциальной системе она будет приводить к таким же последствиям, как и реальная сила той же величины.

Мы уже упоминали об ощущениях наблюдателя в неинерциальной системе (в автобусе, например), связанных с ее торможением или ускорением. Поясним еще действие рассмотренной силы инерции на следующем примере. Рассмотрим тележку с укрепленным на ней кронштейном, к которому подвешен на нити шарик (рис. 9.3). Пока тележка покоится или движется без ускорения, нить расположена вертикально и сила тяжести Р уравновешивается натяжением нити F_H. Приведем теперь тележку в поступательное движение с ускорением А. Нить отклонится от вертикали на такой угол, чтобы результирующая сил Р и F_H сообщала шарику ускорение, равное А, т. е. в инерциальной системе отсчета угол отклонения нити определяется условием, которое, как и должно быть, является следствием второго закона Ньютона. В неинерциальной системе отсчета, связанной с тележкой, шарик покоится, несмотря на то, что результирующая сил

Р и Fн отлична от нуля. Отсутствие ускорения шарика по отношению к этой системе отсчета можно формально объяснить тем, что кроме сил Р и F_H, равных в сумме mА, на шарик действует еще и сила инерции F_in = -mА.

Силы инерции во вращающейся системе отсчета. Рассмотрим теперь случай вращающейся неинерциальной системы и для определенности рассмотрим ситуацию,

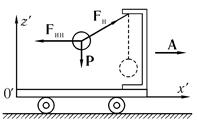
Рис. 9.3

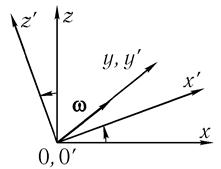
Рис. 9.4

когда неинерциальная система К' вращается с угловой скоростью ω вокруг оси у', совпадающей с осью у инерциальной системы К. Будем полагать также, что начала

отсчета этих систем совпадают (рис. 9.4). Наша цель — записать уравнение

движения материальной точки в неинерциальной системе К' в виде второго

закона Ньютона (9.7).

В инерциальной системе К уравнение движения имеет обычный вид

m a = F,

где а — ускорение рассматриваемой материальной точки в системе К. Вычитая его из уравнения (9.7) (из левой части одного — левую часть другого,

из правой части — правую), получим

F _in= -m(a - a '). (9.8)

Это выражение для силы инерции является обобщением выражения (9.6)

для F_in в случае прямолинейного движения неинерциальной системы отсчета. Для поступательного движения неинерциальной системы а - а ' = А.

Итак, в общем случае сила инерции равна произведению массы тела на

взятую с обратным знаком разность его ускорений по отношению к инерциальной и неинерциальной системам отсчета. При поступательном движении неинерциальной системы К' относительно инерциальной системы К эта разность равна переносному ускорению А, т. е. ускорению начала отсчета системы К1. Рассмотрим в качестве примера относительно простой случай.

Пусть материальная точка во вращающейся системе К' движется в плос-

плоскости х'z' по окружности радиуса R с постоянным модулем скорости v '

(рис. 9.5). В неинерциальной системе К' ускорение материальной точки а ' — это центростремительное ускорение, направленное к центру вращения и равное по

модулю а' = v'²/R.

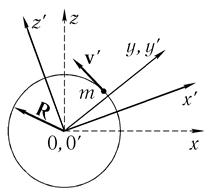
рис. 9.5

В инерциальной системе К материальная точка движется по той же самой окружности, но модуль ее скорости в этой системе определяется суммой v' + v, где v = ωR — скорость движения по окружности в инерциальной системе той точки вращающейся системы К',

в которой находится рассматриваемая материальная точка (мы рассматриваем случай, когда v и v ' направлены в одну сторону).

Следовательно, в инерциальной системе К ускорение материальной точки

а — это также центростремительное ускорение, направленное к центру вращения и по модулю равное

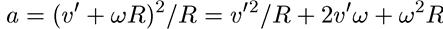
(9.9)

Воспользуемся теперь определением (9.8) и найдем следующее выражение

для модуля силы инерции в рассматриваемом случае:

F_in = m(а - а') = mω²R + 2mv'ω. (9.10)

В соответствии с (9.8) направление найденной силы инерции противоположно направлению разности векторов а - а', направленных в сторону оси вращения. Поскольку, согласно (9.9), модуль а больше модуля а', то разность центростремительных ускорений а - а' направлена к оси вращения, а следовательно, F_in направлена от оси вращения. Окончательно, силу инерции (9.10) можно представить как сумму двух сил, имеющих специальные названия:

F _in = F c + F _K. (9.11)

Здесь F c — центробежная сила инерции

F c = mω² R. (9.12)

В данном случае R — радиус-вектор, проведенный к материальной точке из

начала координат, потому что точка движется в плоскости х'О'z'. В общем

случае это вектор, проведенный от оси вращения к точке в плоскости траектории и его модуль R дает расстояние материальной точки от оси вращения.

Центробежная сила инерции (9.12) действует на тело во вращающейся

системе отсчета независимо от того, покоится тело в этой системе или движется относительно нее. Величина и направление этой силы определяются движением системы отсчета, т. е. переносным ускорением. В этом отношении она подобна силе инерции при поступательном движении системы. Однако, центробежная сила зависит еще и от положения тела во вращающейся системе; она не обладает пространственной однородностью. Центробежную силу инерции необходимо учитывать при точном решении задач о движении тел относительно земной поверхности — ее учет приводит, в частности, к небольшим поправкам к силе тяжести (эти поправки составляют доли процента).

Сила F_K в формуле (9.11) называется силой Кориолиса, или кориолисовой

силой инерции. Для рассмотренного нами частного случая, когда направление скорости движения материальной точки перпендикулярно оси вращения, ее модуль равен 2mv'ω и она направлена вдоль R. В общем случае выражение для силы Кориолиса имеет вид

F _K = 2m[ v ' ω ], (9.13)

где ω — вектор угловой скорости. Отличительной особенностью силы Кориолиса (9.13) является то, что она действует только на движущиеся относительно вращающейся системы отсчета тела. Она пропорциональна векторному произведению v ' и ω, то есть перпендикулярна обоим этим векторам, и ее направление определяется по правилу винта.

Влияние силы Кориолиса следует учитывать, в частности, при истолковании некоторых явлений, связанных с движением тел относительно земной поверхности. Например, летящий снаряд испытывает отклонения, обусловленные кориолисовыми силами инерции. В северном полушарии при горизонтальном полете, независимо от направления, снаряд будет отклоняться вправо, а в южном полушарии — влево. По этой же причине в нашем полушарии у рек подмывается преимущественно правый берег, в южном полушарии — левый.

Итак, в инерциальной системе отсчета ускорение тела определяется «реальными» силами, действующими со стороны других тел (и полей). В неинерциальной системе для определения относительного ускорения, т. е. относительно этой системы, надо добавить силы инерции.

В общем случае система отсчета может двигаться относительно инерциальной (которую мы условно можем считать неподвижной, «абсолютной»)

поступательно и одновременно вращаться. Связь между радиусами-векторами частицы в двух системах по-прежнему определяется соотношением

r = R + r '

Скорость в абсолютной системе теперь слагается из трех составляющих.

Изменение вектора r ' определяет движение относительно системы К' — это

относительная скорость. Свой вклад в абсолютную скорость дает движение системы К' относительно системы К — это скорость начала координат системы К'. Но если даже тело неподвижно в системе К' и начало координат этой системы неподвижно в системе К, тело все же будет двигаться относительно К по окружности радиуса r '. Как мы знаем, скорость в этом случае равна величине [ ωr ']. Таким образом, переносная скорость слагается из двух составляющих, связанных соответственно с поступательным движением системы К' и с ее вращением. В результате получаем

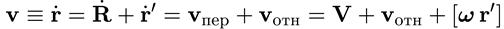
(9.14)

Для нахождения связи ускорений нам надо продифференцировать по времени выражение (9.14). Получаем

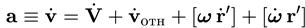
(9.15)

В этом случае также надо учесть наличие двух причин изменения вектора в системе К. Это надо иметь в виду при вычислении второго и третьего членов в формуле (9.14). Не забудем, что

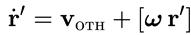
Нетрудно видеть, что мы должны получить такое выражение:

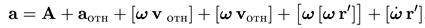
Учитывая, что вклад в векторное произведение дает только перпендикулярная одному из векторов составляющая второго вектора, из правил преобразования двойного векторного произведения

[a[bc]] = b(ac) - c(ab)

получаем

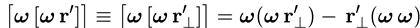
Скалярное произведение двух взаимно перпендикулярных векторов равно

нулю, и от последнего выражения остается одно слагаемое

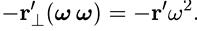
Окончательно имеем

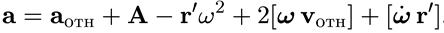
В соответствии с определением (9.8) получаем выражение для суммарной силы инерции в общем случае

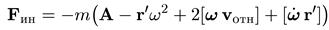
(9.16)

Напомним еще раз, что первый член в этой формуле определяет поступательную силу инерции, второй — центробежную, четвертый — силу инерции, возникающую при неравномерном вращении неинерциальной системы (этот член редко представляет интерес). Все эти силы инерции связаны с переносным ускорением. Особняком

стоит третий член — кориолисова сила инерции, связанная и с движением (вращением) неинерциальной системы, и с движением тела в этой системе.

Одним из любопытных проявлений сил инерции является состояние невесомости. Представим себе, что кто-то стоит на весах в кабине покоящегося лифта (рис. 9.6 а).

Вес — это сила, с которой тело действует на опору, по модулю равная (в

соответствии с третьим законом Ньютона) силе, с которой опора действует

на тело. Обозначим ее N. Когда лифт покоится, сила N уравновешивает

силу тяжести, то есть N = mg. Теперь представим, что лифт свободно падает, то есть движется вниз с ускорением g (рис. 9.6 б). Для наблюдателя в лифте (в неинерциальной системе отсчета) это означает появление «дополнительной» силы инерции F_in= - mg. Эта сила направлена вверх и в точности уравновешивает силу тяжести, так что никакого взаимодействия человека с опорой весов не будет, что и означает обращение его веса в нуль.

Таким образом, возникающее в рассмотренных условиях состояние невесомости

связано с тем, что силы инерции компенсируют силу тяжести.

Аналогичная компенсация гравитационного притяжения к Земле силой инерции происходит и при рассмотрении явлений относительно космического корабля,

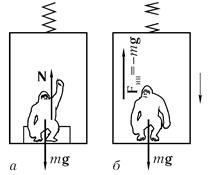
Рис. 9.6

вращающегося вокруг Земли. В этом случае притяжение к Земле компенсируется центробежной силой инерции (рис. 9.7). В самом деле, центробежная сила инерции, действующая на обитателя космического корабля, равна

(см. (9.12))

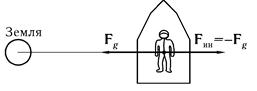
Рис.9.7

F _in = mω² R, (9.17)

где m — масса космонавта, ω — угловая скорость его вращения вместе с кораблем вокруг Земли и R — его радиус-вектор относительно центра Земли. Предположим, что корабль летит по круговой орбите. Это означает, что летящий вместе с кораблем космонавт испытывает в системе, связанной с Землей, центростремительное ускорение ω²R, направленное к центру Земли и связанное с силой притяжения к Земле F _g вторым законом Ньютона (если считать Землю инерциальной системой)

mω² R = Fg.

Сравнивая это равенство с (9.17), мы видим, что сила инерции равна по величине и противоположна по направлению силе притяжения космонавта к Земле. То есть в этом случае, как и в примере с лифтом, возникает состояние невесомости. Спутник свободно падает на Землю, но благодаря большой начальной скорости «никак не может на нее упасть» и в результате движется по окружности.