Приняв гипотезу о едином четырехмерном пространстве-ремени, или четырехмерном мире, мы должны пересмотреть классическую механику Ньютона, исправить ее, сделав инвариантной не относительно преобразований Галилея, а относительно преобразований Лоренца. Такую программу пересмотра динамики материальной точки в классической механике выполнил Минковский, создавший релятивистскую динамику материальной точки.
Чтобы перейти в обычном трехмерном пространстве к геометрически естественным величинам (не зависящим от выбора системы декартовых координат, как координаты точки или компоненты вектора), вводят понятия трехмерных векторов а, b и т.д. и операции над этими векторами, в частности длина вектора а равна
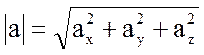
и косинус угла 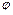 между векторами а и b равен
между векторами а и b равен
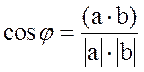 ,
,
где
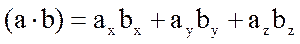
- скалярное произведение векторов а в b. В частности, квадрат длины радиус-вектора г точки М с координатами x,y,z, в некоторой декартовой системе координат, который имеет декартовы компоненты г (x, у, z), равен 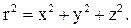
В четырехмерном мире для мгновенного точечного события М с координатами x,y,z,t в некоторой инерциальной системе отсчета можно ввести "4-радиус-вектор" c компонентами
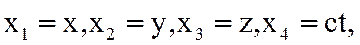
причем квадрат длины этого вектора равен
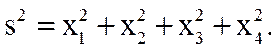
Мгновенной скорость материальной точки
не является лоренц-инвариантной величиной, поэтому Минковский вместо нее в четырехмерном мире ввел релятивистски инвариантную "4-скорость", которая имеет компоненты
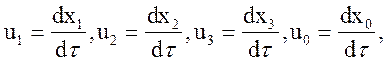
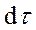 - интервал так называемого собственного времени материальной точки, связанный с ds - релятивистским интервалом между двумя близкими мгновенными точечными событиями, характеризующими два бесконечно близких состояния движения движущейся точки
- интервал так называемого собственного времени материальной точки, связанный с ds - релятивистским интервалом между двумя близкими мгновенными точечными событиями, характеризующими два бесконечно близких состояния движения движущейся точки
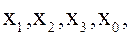 и
и
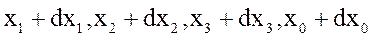
соотношением
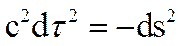 , т.е.
, т.е.
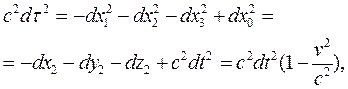
где v - обычная мгновенная скорость материальной точки. Так что 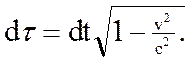
Аналогичным образом релятивистски инвариантное "4-ускорение " Минковский определил следующим образом:
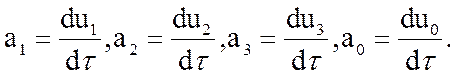
Основные уравнения релятивистской динамики материальной точки в релятивистской механике Минковский записал следующим образом:
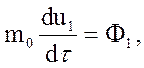
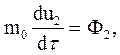
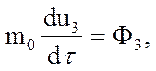
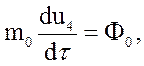
где 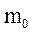 - так называемая "масса покоя" материальной точки
- так называемая "масса покоя" материальной точки
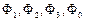 - компоненты так называемой "4-силы " Минковского.
- компоненты так называемой "4-силы " Минковского.
Покажем теперь, как уравнения Минковского релятивистской динамики материальной точки связаны с обычными уравнениями Ньютона для материальной точки. Прежде всего очевидно, что
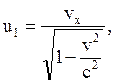
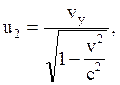

так что
т.е. 4-скорость всегда имеет постоянную величину, чисто мнимую, по модулю равную с.
Используя найденные формулы для компонент 4-скорости и формулу для дифференциала собственного времени, имеем следующие
уравнения движения:
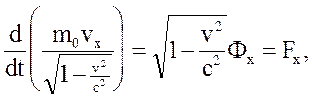
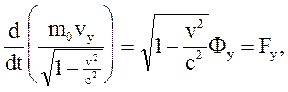
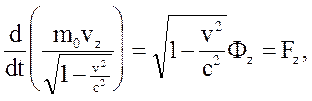
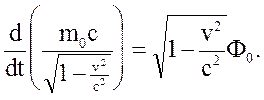
Три уравнения, в которые входят 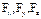 легко сопоставить с уравнениями Ньютона. Нужно только предположить, что теперь масса m материальной точки зависит от скорости по закону
легко сопоставить с уравнениями Ньютона. Нужно только предположить, что теперь масса m материальной точки зависит от скорости по закону
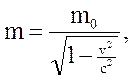
а импульс движущейся материальной точки определяется формулой 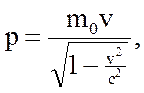
где v - вектор мгновенной скорости материальной точки.
Четвертое уравнение, в которое входит 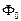 , оказывается, выражает уравнение баланса кинетической энергии материальной точки. Чтобы в этом убедиться, умножим уравнения Минковского на
, оказывается, выражает уравнение баланса кинетической энергии материальной точки. Чтобы в этом убедиться, умножим уравнения Минковского на 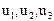 и на -
и на - 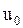 , соответственно и сложим. Получим тогда уравнение
, соответственно и сложим. Получим тогда уравнение
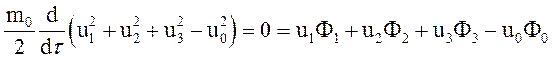
Отсюда можно найти 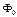 . Имеем
. Имеем
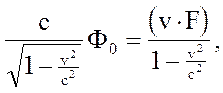
где 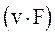 - мгновенная мощность, развиваемая силой, действующей на рассматриваемую материальную точку. Таким образом,
- мгновенная мощность, развиваемая силой, действующей на рассматриваемую материальную точку. Таким образом,
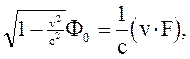
и потому рассматриваемое четвертое уравнение примет вид:
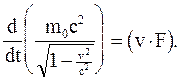
Таким образом, величину
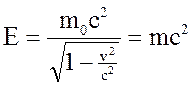
следует считать энергией движущейся материальной точки. Если
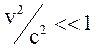 ,
,
то приближенно получаем
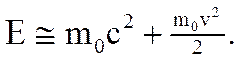
Второе слагаемое есть классическая кинетическая энергия материальной точки
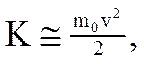
а первое слагаемое - так называемая "энергия покоя". Кинетической энергией материальной точки в релятивистской механике называют величину 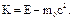
Приведем еще одно важное соотношение, связывающее импульс и энергию релятивистской материальной точки. Имеем
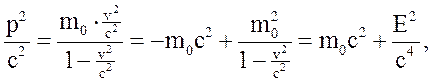
так что имеем формулу
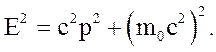
В заключение заметим, что описываемое релятивистское обобщение классической механики материальной точки сказалось полезным при применении к электронам и другим элементарным частицам, и, как показали эксперименты, очень хорошо описывают механические движения.
Вместе с тем, здесь следует отметить, что попытки релятивистского обобщения уравнений классической механики Ньютона для системы даже двух материальных точек в релятивистской механике не увенчались успехом, здесь она столкнулись с серьезными противоречиями и непреодолимыми трудностями.
Некоторые зависимости механики
Механика.
Кинематика.
| Обозн. | Изм. | Смысл |
| S | м | пройденный путь |
| v | м/с | скорость |
| t | с | время |
| x | м | координата |
| a | м/с2 | ускорение |
| w | с-1 | угловая скорость |
| T | с | период |
 | Гц | частота |
| e | с-2 | угловое ускорение |
| R | м | радиус |
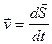 ,
, 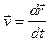 ,
, 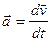
Равномерное движение: 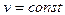
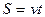 ,
, 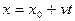 ;
;
 a=const,
a=const, 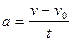 ,
, 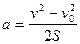 ;
;
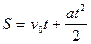 ,
, 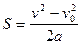 ; v=v0+at,
; v=v0+at, 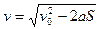 ;
;
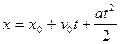 ;
;
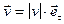
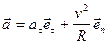 ,
, 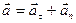
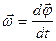 ,
, 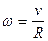 ,
, 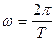 ;
; 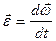 ;
;
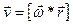 ,
, 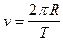 ;
; 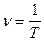 ,
, 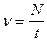 ;
;
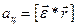 ,
, 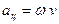 ,
, 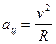 ,
, 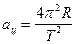 ;
;
Динамика и статика.
| Обозн. | Изм. | Смысл |
| F | Н | сила |
| P | кг*м/с | импульс |
| a | м/с2 | ускорение |
| m | кг | масса |
| v | м/с | скорость |
| p | Н | вес тела |
| g | м/с2 | ускорение свободного падения |
| E | Дж | энергия |
| A | Дж | работа |
| N | Вт | мощность |
| t | с | время |
| I | кг*м2 | момент инерции |
| L | кг*м2/с | момент импульса |
| M | Н*м | момент силы |
| w | с-1 | угловая скорость |
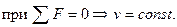
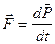 ,
, 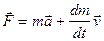 , при m=const è
, при m=const è 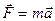
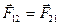
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц,где а- ускорение в неинерциальной а0- в инерциальной системе отчета.
Силы разной природы.
Скорость центра масс 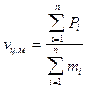 ;
;
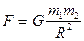 ,
,
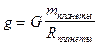 - ускорение свободного падения на планете.
- ускорение свободного падения на планете.
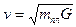 - первая космическая скорость.
- первая космическая скорость.
Вес тела.
p=mg - вес тела в покое.
p=m(g+a) - опора движется с ускорением вверх.
p=m(g-a) - опора движется с ускорением вниз.
p=m(g-v2/r) - движение по выпуклой траектории.
p=m(g+v2/r) - движение по вогнутой траектории.
Сила трения.
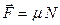 ,
,
Закон Гука.
Fупр=–kx, - сила упругости деформированной пружины.
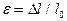 - относительное продольное удлинение (сжатие)
- относительное продольное удлинение (сжатие)
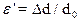 - относительное поперечное удлинение (сжатие)
- относительное поперечное удлинение (сжатие)
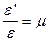 , где m- коэффициент Пуассона.
, где m- коэффициент Пуассона.
Закон Гука: 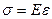 , где Е- модуль Юнга.
, где Е- модуль Юнга.
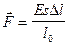
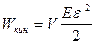 , кинетическая энергия упругорастянутого (сжатого) стержня. (V- объем тела)
, кинетическая энергия упругорастянутого (сжатого) стержня. (V- объем тела)
Динамика и статика вращательного движения.
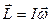 - момент импульса
- момент импульса
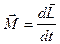 ;
; 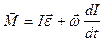 - момент силы
- момент силы
L=const - закон сохранения момента импульса.
M=Fl, где l- плечо
I=I0+mb2 - теорема Штейнера
| система | ось | I |
| точка по окружности | ось симметрии | mR2 |
| стержень | через середину | 1/12 mR2 |
| стержень | через конец | 1/3 mR2 |
| шар | через центр шара | 2/5 mR2 |
| сфера | через центр сферы | 2/3 mR2 |
| кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
| диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия тел 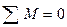
Законы сохранения.
P=mv; - импульс тела.
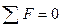
Ft=DP
Потенциальная и кинетическая энергия. Мощность.
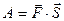 - работа силы F
- работа силы F
A=DE
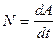 - мощность
- мощность
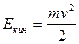 - кинетическая энергия
- кинетическая энергия
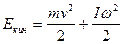 - кинетическая энергия вращательного движения.
- кинетическая энергия вращательного движения.
Ep=mgh - потенциальная энергия поднятого над землей тела.
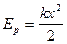 - потенциальная энергия пружины
- потенциальная энергия пружины
Eк1+Eр1=Eк2+Eр2
 2015-02-04
2015-02-04 1075
1075

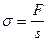 -
-