Динамика твердого тела

Пусть на материальную точку действует сила 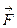. Умножим векторно правую и левую части уравнения движения 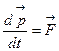этой точки на радиус-вектор 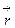точки приложения силы: .

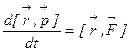Так как 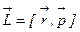и 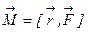, то заменяя, получим основное урав­нение динамики вращательного движе­ния материальной точки: .

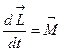Это уравнение легко обобщить на твердое тело, еслипод 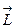и 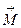понимать суммарный момент импульсов частиц 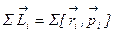, из которых состоит тело, и суммарный момент сил, 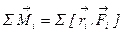, действующих на эти частицы. Приведем различные формы записи этого уравнения при неизменном моменте инерции (J=const):

.

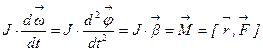Формально все соотношения, описывающие динамику вращательного движения, можно по­лучить из соответствующих соотношений дина­мики поступательного движения материальной точки, если в последних заменить массу тела на момент инерции, силу – на момент силы, им­пульс точки – на момент импульса тела, а ли­нейные скорость и ускорение – на угловые ско­рость и ускорение.

Из основного уравнения динамики для вращательного движения 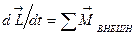для замкнутой системы (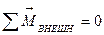) следует закон сохранения момента импульса: в инерциальной системе отсчета момент им­пульса замкнутой системы частиц остается по­стоянным как по величине, так и по направле­нию, т.е. .

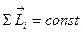В основе закона сохранения момента импульса лежит свойство изотропности (равноправности всех направлений) пространства, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора направлений осей координат инерциальных систем отсчета..