Связь напряженности электрического поля и потенциала

Теорема о циркуляции вектора .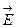

И напряжённость и потенциал описывают один объект – электростатическое поле. Найдем связь между ними, исходя из выражения для работы в дифференциальной форме: .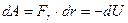

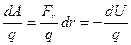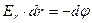Если поделить это выражение на величину пробного заряда q, то получим или или 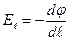для одномерного случая. В общем виде это выражение записывается как: 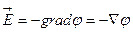(произносится так: «напряженность поля 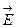равна со знаком минус градиенту потенциала φ»), где 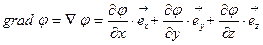. Можно также вычислить разность потенциалов двух точек поля: 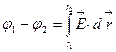. Физический смысл имеет разность потенциалов, она численно равна работе поля при перемещении единичного заряда из одной точки поля в другую; начало отсчёта потенциала (т.е. где положить его равным нулю) выбирается произвольно из соображений удобства в рамках конкретной задачи. Например, выбирают потенциал, равным нулю на бесконечности. Тогда потенциал в некоторой точке поля численно равен работе поля при перемещении единичного заряда из этой точки в бесконечность: 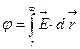. Если единичный заряд возвращается в начальную точку, то работа электростатических сил по замкнутому контуру равна нулю: 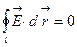. Это соотношение носит название теоремы о циркуляции, а сам интеграл 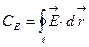называется циркуляцией вектора 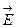по замкнутому контуру ℓ.