Отношение используется как термин для обозначения связи между предметами или понятиями (объектами данной предметной области). Таким образом, отношение - это свойство пар, троек, четверок и т.д. объектов.
Подмножество R декартового произведения множеств 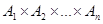 называется отношением степени n (n-арным отношением).
называется отношением степени n (n-арным отношением).
Мощность множества кортежей, входящих в отношение R, называют мощностью отношенияR.
Пусть f 1 - отношение из А в С, 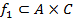 и f 2– отношение из С в В,
и f 2– отношение из С в В, 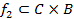 , тогда композицией отношений
, тогда композицией отношений 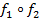 называется отношение
называется отношение
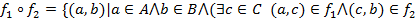 )}.
)}.
Пример:
C={2, 3}.
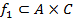 , f 1={(1, 2), (1, 3), (2, 2), (3, 2)}
, f 1={(1, 2), (1, 3), (2, 2), (3, 2)}
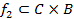 , f 2={(2, 0), (2, 1), (3, 0)}
, f 2={(2, 0), (2, 1), (3, 0)}
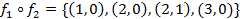
Бинарное отношение 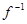 называется обратным к f, если x
называется обратным к f, если x 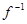 y тогда и только тогда, когда yfx.
y тогда и только тогда, когда yfx.
Пусть f 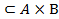 (f отношение из А и В). Ядром отношенияf называется композиция отношения f и обратного для него отношения
(f отношение из А и В). Ядром отношенияf называется композиция отношения f и обратного для него отношения 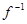 , т.е.
, т.е. 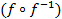 .
.
Пример:
Пусть A ={0, 1}, B={К, Л, О}.
f 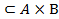 , f 1={(0, К), (0, Л), (1, К), (1, О)}. Найти ядро отношения f, т.е.
, f 1={(0, К), (0, Л), (1, К), (1, О)}. Найти ядро отношения f, т.е. 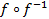 .
.
Решение:
Найдём обратное отношение 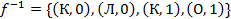 . Затем найдём композицию отношения f и обратного для него отношения
. Затем найдём композицию отношения f и обратного для него отношения 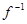 :
: 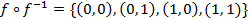 .
.
Рассмотрим свойства бинарных отношений (отношений степени 2).Если пара (x, y) 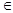 f, то говорят, что элемент x находится в отношении f с элементом y, записывают xfy.
f, то говорят, что элемент x находится в отношении f с элементом y, записывают xfy.
Бинарное отношение f называется рефлексивным, если для любого x 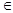 А, пара (x, x)
А, пара (x, x) 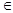 f, что означает что всякий элемент из множества А находится в отношении сам с собой.
f, что означает что всякий элемент из множества А находится в отношении сам с собой.
Т.е., f – рефлексивно, если 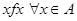 (например, f - «жить в одном городе»);
(например, f - «жить в одном городе»);
Бинарное отношение называется антирефлексивным, если для всех x 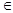 А, (x, x)
А, (x, x) 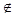 f.
f.
Т.е., f – антирефлексивно, если ни для какого 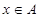 не выполняется
не выполняется 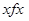 (например, f - «быть сыном»).
(например, f - «быть сыном»).
Бинарное отношение называется симметричным, если из того, что (x, y) 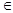 f следует, что (y, x)
f следует, что (y, x) 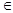 f.
f.
Т.е., f – симметрично, если 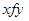 влечёт
влечёт 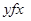 (например, f - «работать на одной фирме»);
(например, f - «работать на одной фирме»);
Бинарное отношение называется антисимметричным,если из того, что (x, y) 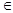 f и (y, x)
f и (y, x) 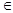 F следует, что x = y.
F следует, что x = y.
Т.е., f – антисимметрично, если ни для каких различающихся элементов x и y (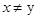 ) не выполняется одновременно
) не выполняется одновременно 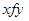 и
и 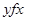 (например, f - «быть дочерью»);
(например, f - «быть дочерью»);
Бинарное отношение называется асимметричным,если по крайней мере одно из соотношение (x, y) 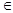 f или (y, x)
f или (y, x) 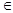 f не выполняется.
f не выполняется.
Бинарное отношение называется транзитивным, если из того, что (x, y) 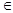 f и (y, z)
f и (y, z) 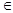 f, следует, что (x, z)
f, следует, что (x, z) 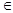 f, (например, R - «быть младше»).
f, (например, R - «быть младше»).
Бинарное отношение называется линейным (связным),если для всех 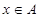 и
и 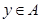 либо (x, y)
либо (x, y) 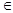 f либо (y, x)
f либо (y, x) 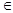 f.
f.
Пример: 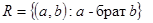 :
:
· не рефлексивно и антирефлексивно, т.к. ни для какого a не выполняется «a брат a»;
· не симметрично, т.к. в общем случае между братом a и сестрой b имеет место 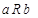 , но не
, но не 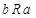 ;
;
· не антисимметрично, т.к. если a и b – братья, то 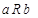 и
и 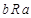 , но
, но 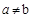 ;
;
· транзитивно, если называть братьями людей, имеющих общих родителей (отца и мать).
Из множества всех отношений, в зависимости от свойств которыми они обладают, выделяют определенные классы отношений.
Отношение R на множестве 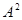 называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности и транзитивности.
называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности и транзитивности.
Обычно отношение эквивалентности обозначают знаком «=» или «≈» и говорят, что оно (отношение) задано на множестве А (а не на 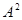 ). Таким образом, для отношения эквивалентности выполняются следующие условия:
). Таким образом, для отношения эквивалентности выполняются следующие условия:
-
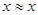 для всех
для всех 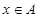 (рефлексивность);
(рефлексивность); - если
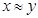 , то
, то 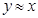 (симметричность);
(симметричность); - если
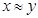 и
и 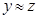 , то
, то 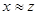 (транзитивность).
(транзитивность).
Отношение R на множестве 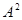 называется отношением (частичного) порядка, если оно обладает свойствами рефлексивности, антисимметричности и транзитивности.
называется отношением (частичного) порядка, если оно обладает свойствами рефлексивности, антисимметричности и транзитивности.
Обычно отношение порядка обозначают знаком 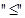 . Если для двух элементов x и y выполняется
. Если для двух элементов x и y выполняется 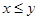 , то говорят, что x "предшествует" y. Таким образом, для отношения порядка выполняются следующие условия:
, то говорят, что x "предшествует" y. Таким образом, для отношения порядка выполняются следующие условия:
-
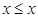 для всех
для всех 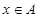 (рефлексивность);
(рефлексивность); - если
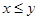 и
и 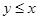 , то
, то 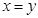 (антисимметричность);
(антисимметричность); - если
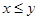 и
и 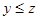 , то
, то 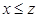 (транзитивность).
(транзитивность).
Кроме того, к отношениям порядка относятся:
1. отношение квазипорядка (предпорядка), обладающее свойствами рефлексивности и транзитивности;
2. отношение строгого порядка, обладающее свойствамиантирефлексивности, асимметричности и транзитивности;
3. отношение линейного (полного) порядка, обладающее наряду со свойствамиотношения частичного порядка свойством линейности.
Отношение R на декартовом произведении двух множеств 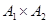 называется функциональным отношением, если оно обладает следующим свойством: если
называется функциональным отношением, если оно обладает следующим свойством: если 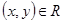 и
и 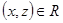 , то
, то 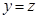 (однозначность функции).
(однозначность функции).
Обычно, функциональное отношение обозначают в виде функциональной зависимости - 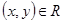 тогда и только тогда, когда
тогда и только тогда, когда 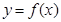 .
.
 2015-02-04
2015-02-04 3623
3623
