2015-02-04
784
Выведем также закон сохранения момента количества движения, но отметим, что он является следствием законов сохранения массы (1.4.12) и импульса (1.6.4).
Напомним определение момента. Момент вектора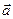 
(рис.1.11) относительно начала координат равен
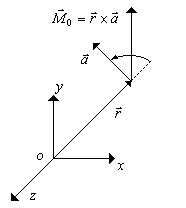
Рис.1.15. Момент вектора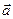
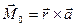, (1.6.5)
где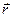 
радиус-вектор, определяющий точку приложения вектора 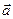. Вектор 
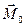направлен по нормали к плоскости, определяемой векторам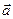и и 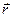, так, что, глядя с конца вектора 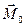, видим поворот от вектора 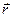к вектору 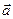, происходящим против часовой стрелки. Модуль вектора М0 равен
.
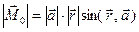В матричной форме векторное произведение записывается в виде
,
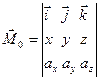или
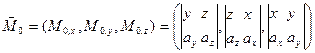, (1.6.6)
т.е. проекции вектора 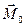на координатные оси численно равны записанным определителям.
Запишем закон сохранения момента количества движения по аналогии с уравнением закона изменения количества движения. С этой целью каждый вектор уравнения (1.6.4) умножим на 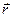(слева):
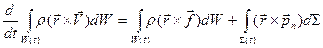. (1.6.7)
Полученное векторное уравнение эквивалентно трём скалярным уравнениям, которые можно выписать, проецируя слагаемые, входящие в уравнение (1.6.7), на координатные оси. Например, в проекции на ось z имеем
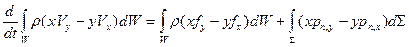. (1.6.8)
Интегральная форма уравнения (1.6.8) используется главным образом в гидромашиностроении при расчётах вращающихся рабочих колёс турбин и насосов.
