Закон изменения кинетической энергии

Изменение кинетической энергии жидкого объёма за единицу времени равно мощности всех внешних и внутренних (поверхностных и массовых) сил, действующих на этот объём жидкости. Кинетическая энергия бесконечно малого объёма 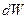жидкости равна 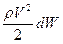, тогда кинетическая энергия объёма 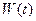будет равна:

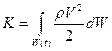. (1.6.9)

Мощность силы равна скалярному произведению вектора силы и вектора скорости тела, на которое она действует. Например, на элементарный объём 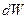действует внешняя массовая сила с плотностью распределения 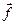, величина этой силы равна 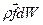. Работа этой силы на перемещении 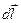равна

.

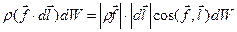Мощность силы найдём как отношение совершаемой ею работы ко времени 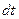, за которое произойдёт перемещение объёма 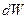на расстояние 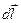. При этом скорость жидкого объём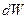а равна 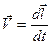. Следовательно, мощность внешней объёмной силы для элементарного объём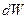а равна 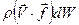. Мощность этой силы при перемещении всего объёма :

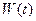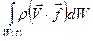. (1.6.10)

Рассуждая аналогично, найдём мощность внешних поверхностных сил, действующих на поверхность 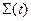, ограничивающую объём :

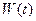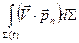, (1.6.11)

где 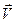- скорость жидкости на поверхности 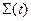в точке, где выделен элемент .

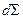Рассчитать работу внешних сил, как правило, не представляется возможным, так как она зависит от поля скорости внутри контрольного объёма, которое, вообще говоря, неизвестно. Поэтому введём функцию 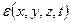- плотность распределения мощности внутренних сил, т.е. работы, которая за единицу времени переходит в тепло и рассеивается (диссипирует) внутри объёма жидкости, имеющего единичную массу. Работа внутренних сил может только уменьшать кинетическую энергию, так как, переходя в энергию беспорядочного теплового движения молекул, соответствующая часть кинетической энергии объёма 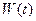уже не участвует в дальнейшем балансе механической энергии. Обычно мощность внутренних сил называют диссипированной, а функцию e диссипативной. Уменьшение кинетической энергии объёма 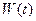за счёт работы внутренних сил представим в виде:

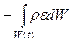. (1.6.12)

Знак минус вводится, чтобы функция e(х,у,z,t) была всегда положительной.

Приравнивая производную от кинетической энергии (1.6.9) сумме мощностей (1.6.10), (1.6.11) и (1.6.12), получаем уравнение, выражающее закон изменения кинетической энергии (баланс механической энергии):

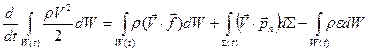. (1.6.13)

Рассмотрим более общий случай. Пусть в контрольном объёме 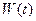, который ограничен контрольной поверхностью 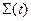, установлена турбина, которую вращает набегающий поток, отдавая ей мощность N_i (поток совершает работу N_i в единицу времени). Индекс i означает, что устройств, изменяющих механическую энергию потока, может быть несколько. Если вместо турбины установить насос, то соответствующая мощность насоса увеличит механическую энергию потока, так что знак N_i зависит от функции устройства внутри контрольного объёма. Запишем при этом уравнение, выражающее баланс механической энергии с учетом источников:

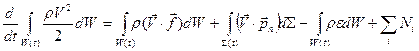. (1.6.14)