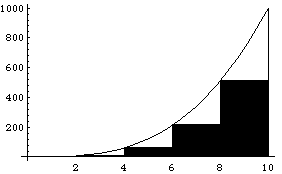
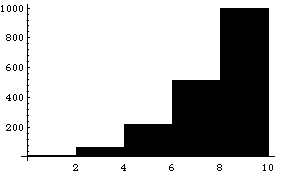Предположим, что некоторая функция задана таблицей значений yi = f (xi), 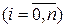 с постоянным шагом аргумента h = xi – xi -1
с постоянным шагом аргумента h = xi – xi -1 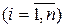 . Для того, чтобы выразить значение производной через значения функции в узлах интерполяции, запишем интерполяционный многочлен Лагранжа степени m, удовлетворяющий условиям Lm (xk) = yk = f (xk),
. Для того, чтобы выразить значение производной через значения функции в узлах интерполяции, запишем интерполяционный многочлен Лагранжа степени m, удовлетворяющий условиям Lm (xk) = yk = f (xk), 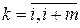 :
:
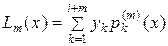 ,
,
где лагранжевы коэффициенты вычисляются как
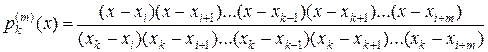 .
.
Дифференцируя этот многочлен, можно получить приближенные значения производных в узлах интерполирования xk 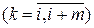 .
.
В частности, для m = 1 получим:
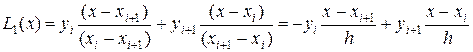 ;
;
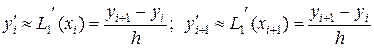 .
.
численный дифференцирование производная интерполяционный
Пусть m = 2. Тогда
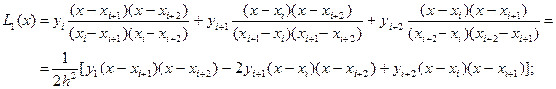
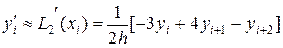 , (5)
, (5)
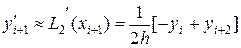 , (6)
, (6)
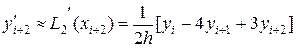 . (7)
. (7)
В целом для отрезка [ x 0, xn ] рекомендуется вычислять производные следующим образом:
а) значение y ¢(x 0) - по формуле (5), где xi = x 0;
б) значения y ¢(xi) 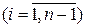 - по формуле (6), где xi +1
- по формуле (6), где xi +1 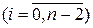 ;
;
в) значение y ¢(xn) - по формуле (7), где xi +2 = xn.
№12 ЧисленДиффМетод неопределенных коэффициентов
Аналогичные формулы можно получить и для случая произвольного расположения узлов. Использование многочлена Лагранжа в этом случае приводит к вычислению громоздких выражений, поэтому удобнее применять метод неопределенных коэффициентов. Он заключается в следующем. Искомое выражение для производной k -гo порядка в некоторой точке х = xi представляется в виде линейной комбинации заданных значений функции в узлах x0, x1,...,xn:
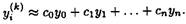 (3.10)
(3.10)
Предполагается, что это соотношение выполняется точно, если функция у является многочленом степени не выше n, т.е. может быть представлена в виде
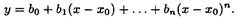
Отсюда следует, что соотношение (3.10), в частности, должно выполняться точно для многочленов у — 1, у = х - х0,..., 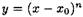 . Подставляя последовательно эти выражения в (3.10) и требуя выполнения точного равенства, получаем систему п + 1 линейных алгебраических уравнений для определения неизвестных коэффициентов с 0, с 1,..., сn.
. Подставляя последовательно эти выражения в (3.10) и требуя выполнения точного равенства, получаем систему п + 1 линейных алгебраических уравнений для определения неизвестных коэффициентов с 0, с 1,..., сn.
Пример. Найти выражение для производной 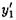 в случае четырех равноотстоящих узлов (n =3).
в случае четырех равноотстоящих узлов (n =3).
Приближение (3.10) запишется в виде
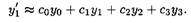 (3.11)
(3.11)
Используем следующие многочлены:
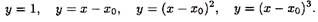 (3.12)
(3.12)
Вычислим их производные:
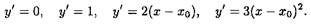 (3.13)
(3.13)
Подставим последовательно соотношения (3.12) и (3.13), соответственно в правую и левую части (3.11) при х = х 1, требуя выполнения точного равенства:
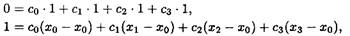
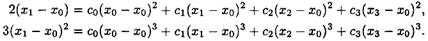
Получим окончательно систему уравнений в виде
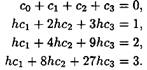
Решив эту систему, получим
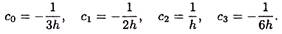
Подставив эти значения в (3.11), найдем выражение для производной:
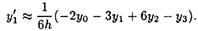
№13
| Формула прямоугольников |
На частичном отрезке [ Xi-1, Xi ] заменим подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно в качестве этой точки выбрать среднюю: Xi-0.5 = Xi - 0.5 H. Тогда получим формулу 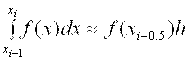 . (2.6) Подставив (2.6) в (2.5), получим составную формулу средних прямоугольников: . (2.6) Подставив (2.6) в (2.5), получим составную формулу средних прямоугольников: 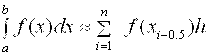 . (2.7) Графическая иллюстрация метода средних прямоугольников представлена на рис. 2.1. . (2.7) Графическая иллюстрация метода средних прямоугольников представлена на рис. 2.1. 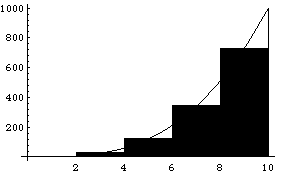 Рис. 2.1.Интегрирование методом средних прямоугольников Погрешность формулы (2.7) определяется выражением Рис. 2.1.Интегрирование методом средних прямоугольников Погрешность формулы (2.7) определяется выражением 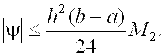 (2.8) Здесь (2.8) Здесь 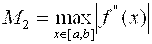 . Таким образом, погрешность формулы (2.7) пропорциональна O(H2). Замечание. Формулу (2.7) можно представить в ином виде: . Таким образом, погрешность формулы (2.7) пропорциональна O(H2). Замечание. Формулу (2.7) можно представить в ином виде: 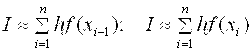 . (2.9) Эти формулы в выражении (2.9) называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 2.2. . (2.9) Эти формулы в выражении (2.9) называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 2.2.
|
А) б)
Рис. 2.2. Метод левых (а) и правых (б) прямоугольников
Однако из-за нарушения симметрии в формулах (2.9) их погрешность значительно больше, чем в методе средних прямоугольников и ~ O(H).
№14
| Формула трапеций |
Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени, то есть  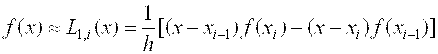 , (2.10) Тогда искомый интеграл запишется следующим образом: , (2.10) Тогда искомый интеграл запишется следующим образом: 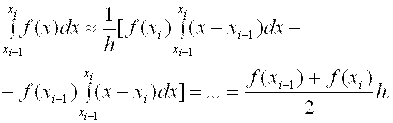 (2.11) После подстановки выражения (2.11) в (2.5) составная формула трапеций примет вид (2.11) После подстановки выражения (2.11) в (2.5) составная формула трапеций примет вид 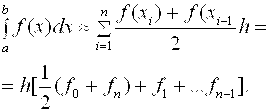 (2.12) Графически метод трапеций представлен на рис. 2.3. (2.12) Графически метод трапеций представлен на рис. 2.3. 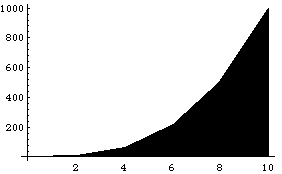 Рис. 2.3.Метод трапеций Погрешность формулы (2.12) определяется выражением: Рис. 2.3.Метод трапеций Погрешность формулы (2.12) определяется выражением: 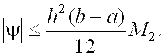 (2.13) Таким образом, погрешность метода трапеций Ψ ~ O(H²), но она в два раза больше, чем для формулы средних прямоугольников. (2.13) Таким образом, погрешность метода трапеций Ψ ~ O(H²), но она в два раза больше, чем для формулы средних прямоугольников. |
№ 15 Метод Парабол он же Симпсона
В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки
(Xj, F (Xj)), где J = I -1; I -0.5; I, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:

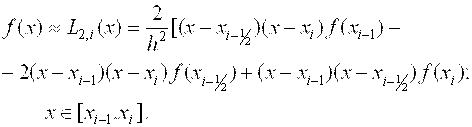 (2.14)
(2.14)
Проведя интегрирование, получим:
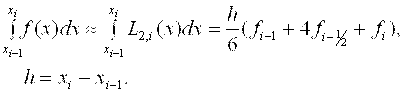
 (2.15)
(2.15)
Это и есть Формула Симпсона или формула парабол. На отрезке
[ A, B ] формула Симпсона примет вид

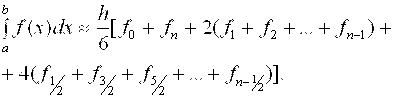 (2.16)
(2.16)
Графическое представление метода Симпсона показано на рис. 2.4.
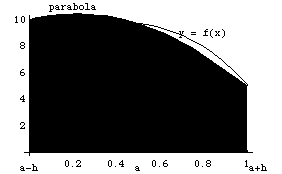
Рис. 2.4. Метод Симпсона
Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:
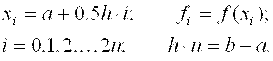 (2.17)
(2.17)
Тогда формула Симпсона примет вид
 (2.18)
(2.18)
Погрешность формулы (2.18) оценивается следующим выражением:
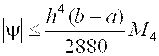 , (2.19)
, (2.19)
Где H·N = B - A, 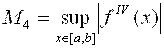 . Таким образом, погрешность формулы Симпсона пропорциональна O (H4).
. Таким образом, погрешность формулы Симпсона пропорциональна O (H4).
Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на Четное число интервалов.
№ 16 Задача Коши методом Эйлера
Пусть дана задача Коши для уравнения первого порядка
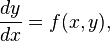
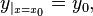
где функция 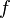 определена на некоторой области
определена на некоторой области 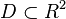 . Решение ищется на интервале
. Решение ищется на интервале 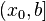 . На этом интервале введем узлы
. На этом интервале введем узлы
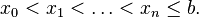
Приближенное решение в узлах 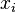 , которое обозначим через
, которое обозначим через 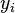 определяется по формуле
определяется по формуле
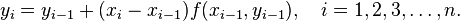
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
 2015-02-04
2015-02-04 1510
1510