Формулировка задачи Коши на сетке 

 ,
, 
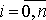
 ,
, 
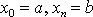
 :
:
Решить систему ОДУ первого порядка:

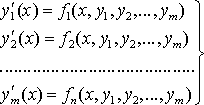
 ,
,
где 
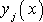
 ,
, 
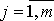
 - неизвестные функции, удовлетворяющие начальным условиям
- неизвестные функции, удовлетворяющие начальным условиям

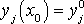
 .
.
Задача Коши в векторной форме:

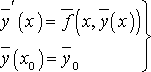
 ,
,
где

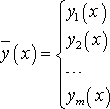
 ,
, 
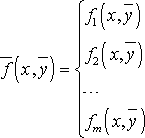
 ,
, 
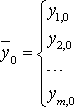
 .
.
Численное решение задачи Коши состоит в том, что на сетке 
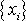
 ,
, 
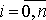
 , требуется получить приближенные значения
, требуется получить приближенные значения 
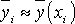
 , где
, где


 .
.
Условия существования и единственности решения данной задачи Коши такие же, как и для ОДУ первого порядка:
Функции  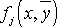  должны быть непрерывными вместе со своими частными производными должны быть непрерывными вместе со своими частными производными  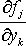  , ,  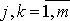  , в некоторой области D в пространстве , в некоторой области D в пространстве  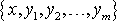  . . |
При выполнении этих условий через точку 
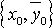
 проходит единственная совокупность кривых:
проходит единственная совокупность кривых:
Величина погрешности при решении систем ОДУ оценивается значением

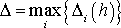
 ,
, 
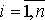
 ,
,
где 
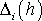
 - погрешность решения на сетке
- погрешность решения на сетке 
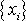
 с шагом h в точке
с шагом h в точке 
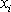
 :
:

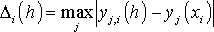
 ,
,
Здесь

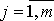
 ,
, 
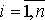
 ;
;

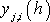
 - приближенное решение;
- приближенное решение;

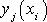
 - точное решение.
- точное решение.
На практике погрешность в точке 
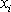
 оценивается по формуле Рунге, аналогичной выражению для одного уравнения.
оценивается по формуле Рунге, аналогичной выражению для одного уравнения.
Численное решение задачи Коши для систем ОДУ 1 

 го порядка методами Рунге
го порядка методами Рунге 

 Кутта ищется по тем же формулам, что и для ОДУ первого порядка. Например, решение методом Рунге
Кутта ищется по тем же формулам, что и для ОДУ первого порядка. Например, решение методом Рунге 

 Кутта 4
Кутта 4 

 го порядка можно найти, если положить:
го порядка можно найти, если положить:

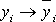
 ,
, 
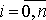
 ;
;

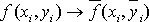
 ;
;

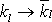
 , где
, где

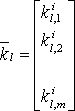
 ,
, 
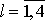
 .
.
В результате получим

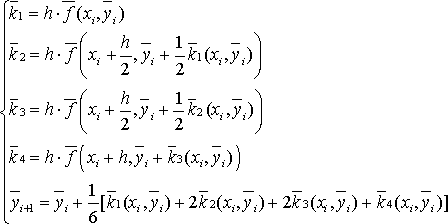
 .
.
Пример. Формулы метода Рунге-Кутта 4-го порядка для системы двух уравнений:

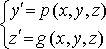
 , н.у.:
, н.у.: 
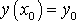
 ,
, 
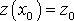
 .
.
Т.е.

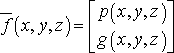
 ,
, 
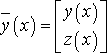
 ,
, 
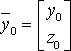
 .
.

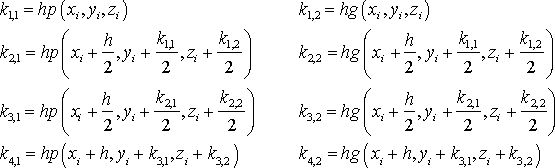
 .
.

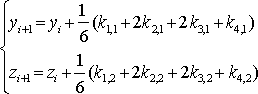
 .
.
№20
| Метод конечных разностей (метод сеток) |  |  |  |
Наиболее эффективно этот метод применяется для линейной краевой задачи, постановка которой для дифференциального уравнения второго порядка имеет вид:
Введем равномерную сетку Определим на этой сетке Сеточные функции:
Запишем основное уравнение системы (21) для фиксированного узла
В каждом внутреннем узле сетки (
Подставим полученные соотношения в (22):
Где обозначено
Приводя подобные члены, получим окончательно:
Общее число неизвестных на сетке равно Граничное условие третьего рода имеет вид (см. урав.(18)):
Разложим функцию
Подставляя найденное значение второй производной в выражение для
Отбрасывая остаточный член и приводя подобные в последнем уравнении, получаем систему линейных уравнений для неизвестных
Исключая из полученной системы
Где параметры
В результате получаем неявную конечно-разностную систему уравнений, записанную в Каноническом виде:
Система (25) - трехдиагональная, для которой разработаны специальные эффективные методы численного решения, например, метод прогонки [1,6,11]. |
№21
| Численные методы решения краевых задач для ОДУ. Постановка задачи для диффернциального уравнения 2-го порядка |  |  |  |
Рассмотрим вначале общую нелинейную постановку краевой задачи для ОДУ второго порядка: 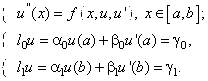 (18) В постановке задачи (18) принята следующая классификация граничных условий: При (18) В постановке задачи (18) принята следующая классификация граничных условий: При 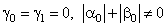 - краевые условия – Однородные; при - краевые условия – Однородные; при 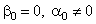 - краевое Условие первого рода на левом конце; при - краевое Условие первого рода на левом конце; при 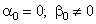 - краевое условие Второго рода на левом конце; при - краевое условие Второго рода на левом конце; при 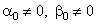 - краевые условия Третьего рода на левом конце. На правом конце отрезка краевые условия классифицируются аналогично. Отметим основное отличие краевой задачи (18) от задачи Коши: в задаче Коши начальные условия задаются в одной точке (как правило, на левом конце отрезка), а в краевой задаче – на обоих концах. Естественно попытаться свести краевую задачу к задаче Коши, т. к. для нее разработаны эффективные приближенные методы решения. Таковым, например, является Метод стрельбы. Для простоты рассмотрим задачу (18) с краевыми условиями первого рода: - краевые условия Третьего рода на левом конце. На правом конце отрезка краевые условия классифицируются аналогично. Отметим основное отличие краевой задачи (18) от задачи Коши: в задаче Коши начальные условия задаются в одной точке (как правило, на левом конце отрезка), а в краевой задаче – на обоих концах. Естественно попытаться свести краевую задачу к задаче Коши, т. к. для нее разработаны эффективные приближенные методы решения. Таковым, например, является Метод стрельбы. Для простоты рассмотрим задачу (18) с краевыми условиями первого рода: 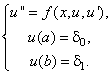 (19) Заменим задачу (19) на следующую задачу Коши: (19) Заменим задачу (19) на следующую задачу Коши: 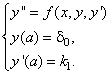 (20) Решаем задачу (20) подходящим методом Рунге-Кутты. Обозначим полученное решение (20) Решаем задачу (20) подходящим методом Рунге-Кутты. Обозначим полученное решение 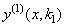 и вычислим величину и вычислим величину 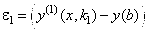 - погрешность решения на правом конце. Корректируем угловой коэффициент - погрешность решения на правом конце. Корректируем угловой коэффициент 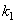 на левом конце в зависимости от знака погрешности, заменяя его на на левом конце в зависимости от знака погрешности, заменяя его на 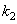 . Находим новое решение . Находим новое решение 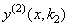 и т. д. до тех пор, пока не выполнится условие и т. д. до тех пор, пока не выполнится условие 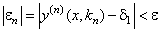 , где , где 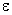 - заданная погрешность. Название метода связано с его геометрической интерпретацией: Стрельба из точки с координатами - заданная погрешность. Название метода связано с его геометрической интерпретацией: Стрельба из точки с координатами 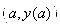 под углом, определяемым угловым коэффициентом под углом, определяемым угловым коэффициентом 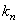 . . |
 2015-02-04
2015-02-04 3308
3308

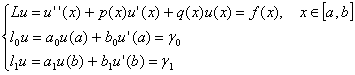
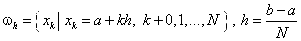 - шаг сетки.
- шаг сетки.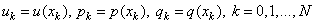 , где
, где 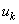 - точное решение на сетке.
- точное решение на сетке.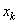 :
: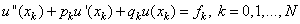 . (22)
. (22)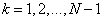 ) аппроксимируем производные по формулам второго порядка точности (см. теор. 4.1 – 4.3):
) аппроксимируем производные по формулам второго порядка точности (см. теор. 4.1 – 4.3):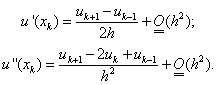
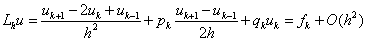 ,
,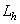 - Сеточный оператор, действующий на сетке. Умножая обе части уравнения на
- Сеточный оператор, действующий на сетке. Умножая обе части уравнения на 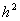 и отбрасывая остаточный член, получим приближение к точному уравнению:
и отбрасывая остаточный член, получим приближение к точному уравнению: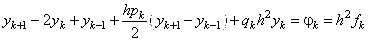 .
.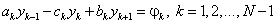 , где
, где 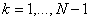 .
. 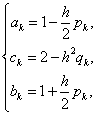
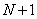 (
(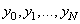 ), а система (23) содержит
), а система (23) содержит 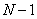 уравнение для неизвестных
уравнение для неизвестных 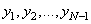 . Недостающие значения должны быть определены из граничных условий. Порядок аппроксимации основного уравнения системы
. Недостающие значения должны быть определены из граничных условий. Порядок аппроксимации основного уравнения системы 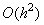 . При постановке задачи с краевыми условиями первого рода порядок аппроксимации всей схемы не ухудшится и будет равен
. При постановке задачи с краевыми условиями первого рода порядок аппроксимации всей схемы не ухудшится и будет равен 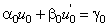 (24)
(24)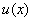 по Тэйлору с центром в точке
по Тэйлору с центром в точке 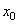 и найдем значение
и найдем значение 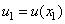 :
: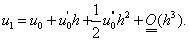
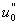 найдем из уравнения (21), аппроксимируя его в точке сетки
найдем из уравнения (21), аппроксимируя его в точке сетки 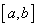 позволяет это сделать):
позволяет это сделать):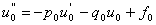 .
.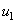 , получаем:
, получаем: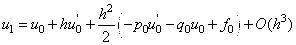 .
.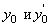 :
: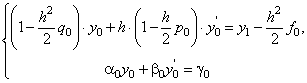
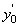 , получаем линейное уравнение, связывающее два сеточных значения
, получаем линейное уравнение, связывающее два сеточных значения 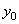 и
и 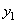 :
: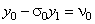 ,
,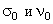 легко выражаются через
легко выражаются через 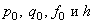 . Аналогично аппроксимируется третье краевое условие на правом конце отрезка, которое приводится к виду
. Аналогично аппроксимируется третье краевое условие на правом конце отрезка, которое приводится к виду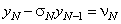 .
.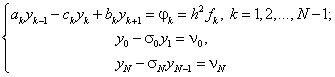 (25)
(25)