Вектор поляризованности

Вектор поляризации — векторная физическая величина, равная дипольному моменту единицы объёма вещества, возникающему при его поляризации, количественная характеристика диэлектрической поляризации^[1].

Обозначается буквой 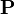, в Международной системе единиц (СИ) измеряется в Кл/м².

Диэлектрическая поляризация обусловлена смещением связанных зарядов вещества во внешнем электрическом поле относительно их расположения при отсутствии внешнего электрического поля. Если выделить какой-либо объём в диэлектрике, то в результате приложения поля на его поверхности могут возникнуть поверхностные электрические заряды 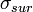. Такие заряды могут возникнуть или благодаря смещению электронной оболочки относительно ядра атома, или же в результате переориентации молекул, которые имеют собственный дипольный момент.

Нормальную к поверхности составляющую вектора поляризации определяют как

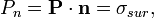
где 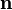— орт нормали к поверхности.

Можно ввести вектор электрической индукции 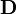, который удобен при описании электрического поля в сплошной среде:

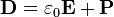(СИ)

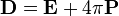(СГС)

Связь с электрическим полем

В основном зависимость между вектором поляризации и электрическим полем, которое обусловило поляризацию, линейна и задается тензором поляризуемости.

.

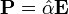Определённые вещества могут быть поляризованными при отсутствии электрического поля. К таким веществам относятся пироэлектрики — кристаллические вещества со спонтанной поляризацией и электреты — аморфные вещества, в которых наведённая полем поляризация может сохраняться на протяжении длительного времени.

В случае переменного электрического поля среда может реагировать на изменение поля с некоторым запозданием. В этом случае вектор поляризации в данный момент зависит от напряжённости приложенного электрического поля в предыдущие моменты времени. В таких случаях говорят о временно́й дисперсии и соотношения между вектором поляризации и электромагнитным полем выглядят как

.

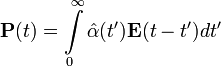Фурье-образы вектора поляризации и напряжённости электрического поля в таком случае связаны линейным соотношением: 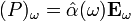, где

.

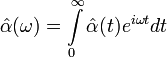Если электромагнитное поле неоднородно в пространстве, как, например, в случае распространения электромагнитных волн, и взаимодействует с возбуждениями в веществе, которые имеют длину волны порядка длины электромагнитной волны, то значение поляризации в определённой точке пространства зависит от значения напряжённости электрического поля в соседних точках пространства. В таких случаях говорят о пространственной дисперсии (укр.)русск..

.

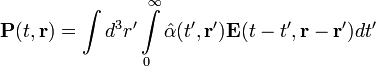В сильных электрических полях зависимость между поляризацией и электрическим полем может отличаться от линейной. Явления, которые при этом возникают изучаются, например, в нелинейной оптике.

12. Условие равновесия заряда на проводнике;

Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение следующих условий:

1. Напряженность поля всюду внутри проводника должна быть равна нулю:

Е = 0. (1.46)

В соответствии с это означает, что потенциал внутри проводника должен быть постоянным (φ = const).

2. Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности:

Е = Еn. (1.47)

Следовательно, в случае равновесия зарядов поверхность проводника будет эквипотенциальной.

Если проводящему телу сообщить некоторый заряд q, то он распределится так, чтобы соблюдались условия равновесия. Представим себе произвольную замкнутую поверхность, полностью заключенную в пределах тела. При равновесии зарядов поле в каждой точке внутри проводника отсутствует; поэтому поток вектора электрического смещения через поверхность равен нулю. Согласно теореме Гаусса сумма зарядов внутри поверхности также будет равна нулю. Это справедливо для поверхности любых размеров, проведенной внутри проводника произвольным образом. Следовательно, при равновесии ни в каком месте внутри проводника не может быть избыточных зарядов – все они распределяются по поверхности проводника с некоторой плотностью σ.

Поскольку в состоянии равновесия внутри проводника избыточных зарядов нет, удаление вещества из некоторого объема, взятого внутри проводника, никак не отразится на равновесном расположении зарядов. Таким образом, избыточный заряд распределяется на полом проводнике также, как и на сплошном, т. е. по его наружной поверхности. На поверхности полости в состоянии равновесия избыточные заряды располагаться не могут. Этот вывод вытекает также из того, что одноименные элементарные заряды, образующие данный заряд q, взаимно отталкиваются и, следовательно, стремятся расположиться на наибольшем расстоянии друг от друга.

13. Электроемкость, конденсаторы. Последовательное и параллельное соединение конденсаторов;

Определение: Формула: Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними

Количественно характеризует способность системы проводников накапливать электрический заряд; Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.

В системе СИ единица электроемкости называется фарад (Ф): 1Ф – это очень большая величина. Электроемкость земного шара равна 709 мкФ. На практике используют дольные единицы: 1 мкФ (микрофарад)=10 -6 Ф; 1 нФ (нанофарад)=10 -9 Ф; 1пФ (пикофарад)=10 -12 Ф.

Система проводников, разделенных диэлектриком, толщина которого мала по сравнению с линейными размерами проводников. Проводники, образующие конденсатор, называются его обкладками.

По типу используемого диэлектрика: бумажные, воздушные, керамические, электролитические, слюдяные, полистирольные; По рабочему напряжению: низковольтные (с напряжением пробоя до 100 В), высоковольтные (с напряжением пробоя до 100 000 В).

Напряжение на обкладках всех конденсаторов одно и то же: U 1 =U 2 =U 3 =…=U n =U; Суммарный заряд батареи равен сумме зарядов на каждом из конденсаторов: q=q 1 +q 2 +q 3 +…+q n; Емкость батареи равна сумме емкостей всех конденсаторов: С=С 1 +С 2 +С 3 +…+С n

Заряд батареи равен заряду каждого из конденсаторов: q 1 =q 2 =q 3 =…=q n =q; Напряжение батареи равно сумме напряжений на всех конденсаторах: U=U 1 +U 2 +U 3 +…+U n; Электроемкость батареи конденсаторов можно определить из соотношения:

Параллельное соединение конденсаторов применяется для увеличения электроемкости системы. Последовательное соединение конденсаторов применяется для увеличения предельного рабочего напряжения батареи.