Решение.
Пример.
Решение.
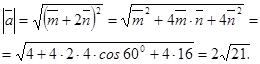
Найти угол 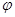 между векторами
между векторами 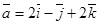 ,
, 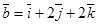 .
.
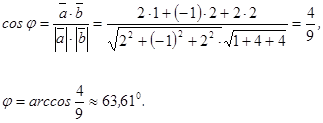
Векторным произведением двух векторов  и
и 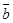 , называется вектор
, называется вектор 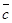 =
=  ×
×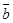 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1. |
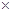
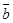 | =
| = 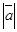 ∙
∙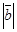 ∙sinφ, где φ – угол между векторами
∙sinφ, где φ – угол между векторами  и
и 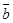 в промежутке [0;1800];
в промежутке [0;1800];
2. 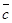
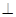
 ,
, 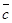
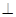
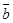 ;
;
3. если смотреть с конца вектора 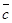 на плоскость, в которой лежат векторы
на плоскость, в которой лежат векторы  и
и 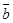 , то кратчайший поворот от вектора
, то кратчайший поворот от вектора  до
до 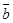 будет виден совершающимся против часовой стрелки (правило правого винта).
будет виден совершающимся против часовой стрелки (правило правого винта).
Применяется векторное произведение для вычисления площадей многоугольников. С помощью векторного произведения можно установить признак параллельности векторов, а именно, два вектора тогда и только тогда взаимно параллельны, когда их векторное произведение равно нулевому вектору. Отметим, что в этом случае удобнее пользоваться признаком: два вектора взаимно параллельны тогда и только тогда, когда их координаты пропорциональны. Оно имеет и другие применения, но в основном в физико-технических задачах.
Из первого пункта определения векторного произведения следуют формулы:
|
|
|
│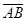
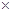
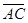 │ = S – площадь параллелограмма ABCD;
│ = S – площадь параллелограмма ABCD;
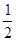 │
│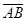
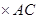 │ = S – площадь треугольника ABC.
│ = S – площадь треугольника ABC.
Векторное произведение обладает свойствами:
1) 
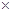
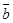 = – (
= – (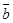
 ); 2)
); 2) 
 (
(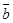 +
+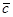 ) = (
) = (
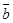 ) + (
) + (
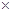
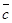 );
);
3) m
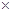 n
n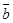 = (m n) (
= (m n) (
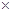
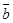 ), где m,n
), где m,n 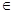 R.
R.
Применяется векторное произведение для вычисления площадей многоугольников. С помощью векторного произведения можно установить признак параллельности векторов, а именно, два вектора тогда и только тогда взаимно параллельны, когда их векторное произведение равно нулевому вектору. Отметим, что в этом случае удобнее пользоваться признаком: два вектора взаимно параллельны тогда и только тогда, когда их координаты пропорциональны. Оно имеет и другие применения, но в основном в физико-технических задачах.
Из первого пункта определения векторного произведения следуют формулы:
│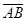
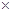
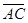 │ = S – площадь параллелограмма ABCD;
│ = S – площадь параллелограмма ABCD;
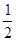 │
│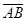
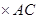 │ = S – площадь треугольника ABC.
│ = S – площадь треугольника ABC.
Векторное произведение обладает свойствами:
1) 
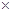
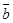 = – (
= – (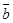
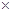
 ); 2)
); 2) 
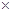 (
(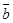 +
+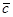 ) = (
) = (
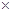
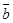 ) + (
) + (
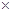
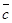 );
);
3) m 
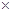 n
n 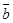 = (m n) (
= (m n) (
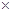
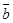 ), где m, n
), где m, n 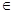 R.
R.
Пользуясь свойствами векторного произведения и его определением, можно получить формулу:

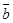 =
= 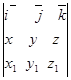 ,
,
где  =
=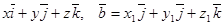 .
.
Пример. Вычислить площадь треугольника с вершинами А(1,1,2), В(0;2;4),С(-1;3;0).
Решение. 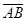 =(0-1; 2-1; 4-2)= (-1; 1; 2),
=(0-1; 2-1; 4-2)= (-1; 1; 2), 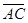 = (-1-1; 3-1; 0-2)= =(-2;2;-2).
= (-1-1; 3-1; 0-2)= =(-2;2;-2).
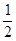 │
│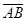
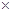
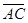 │=
│=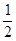 │
│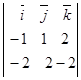
Пример. Вычислить площадь треугольника с вершинами
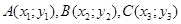 .
.
Решение. Будем считать, что третья координата вершин треугольника равна нулю. Тогда:
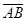 =(
=( ;
; 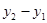 ;0),
;0), 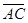 = (
= (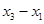 ;
; 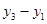 ; 0).
; 0).
│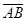
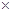
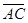 │=
│=
│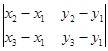 │.
│.
Получили формулу площади параллелограмма со смежными сторонами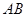 и
и 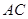 . Формула площади треугольника АВС имеет вид:
. Формула площади треугольника АВС имеет вид:
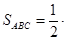 │
│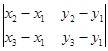 │.
│.
 2014-02-09
2014-02-09 2078
2078