Метод И.С. Гольфарба

Он основан на графическом решении характеристического уравнения:

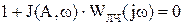
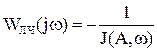или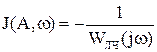

Для определения режима колебаний необходимо построить АФЧХ линейной части и отрицательную инверсную характеристику НЭ (или характеристику НЭ и инверсную отрицательную АФЧХ линейной части). Точка пересечения этих графиков определяет параметры колебаний (амплитуду, частоту). Координаты точки пересечения графиков подставляются в выражение для АФЧХ ЛЧ 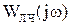и определяется 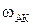, затем координаты точки пересечения и 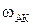подставляются в выражение инверсной отрицательной характеристики НЭ 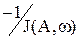и определяется .

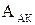Устойчив или нет режим этих колебаний определяется следующим образом: если двигаясь по инверсной отрицательной характеристике НЭ в сторону увеличения амплитуды мы выходим из области, охваченной АФЧХ ЛЧ, то режим автоколебаний – устойчивый.

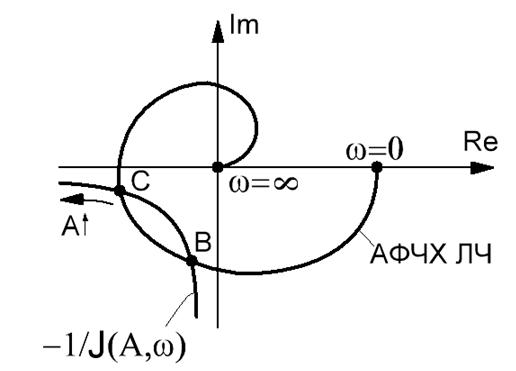
На рисунке в точке С режим устойчивых автоколебаний, в точке B нет.

Если нет пересечения АФЧХ ЛЧ и отрицательной инверсной характеристики НЭ, то режима колебаний нет.

Для однозначной симметричной нелинейной характеристики инверсная частотная характеристика НЭ совпадает с отрицательным отрезком вещественной оси.

Если нелинейная характеристика содержит зону неоднозначности (гистерезиса), то для, например, двухпозиционной релейной характеристики инверсная частотная характеристика проходит параллельно отрицательного отрезка вещественной оси, и отстаёт от него на некоторую величину.

Этот метод позволяет оценить влияние параметров ЛЧ системы на режим колебаний и спроектировать системы, ограничивающие амплитуду автоколебаний или устраняющие их за счёт изменения ЛЧ.

Для определения амплитуды и частоты этим методом АФЧХ ЛЧ и инверсной отрицательной характеристики НЭ желательно строить в одном масштабе, поэтому отрицательную инверсную характеристику НЭ часто строят в масштабе 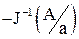, где a – зона нечувствительности или неоднозначности.

Метод Гольдфарба можно использовать для определения параметров автоколебаний и логарифмические АЧХ и ФЧХ. Для этого уравнение характеристического вектора:

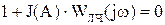
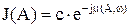
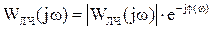
где с – модуль коэффициента передачи НЭ.

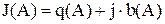
тогда ;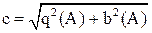

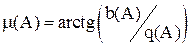
Тогда уравнение характеристического вектора можно разложить на 2.

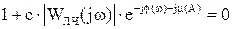
Можно написать уравнение баланса амплитуд и уравнение баланса фаз:

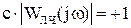и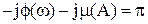

;

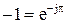Это и есть система баланса амплитуд и фазовых сдвигов.

Для определения параметров колебаний строим по уравнению баланса амплитуд ЛАЧХи ЛЧ и НЭ, а по уравнению баланса фаз ФЧХ ЛЧ и НЭ.

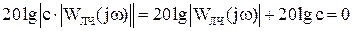
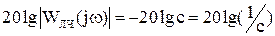
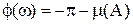
Одновременно выполнение условия баланса амплитуд и баланса фаз обеспечит режим незатухающих колебаний. Графически это выражается в том, что точки характеристик АЧХ и ФЧХ лежат на одной вертикали. Если таких точек нет, то и режим автоколебаний нет.

Для однозначных симметричных нелинейностей условие баланса для логарифмических характеристик можно записать так:

;

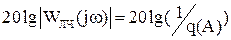а уравнение фазовых характеристик:

,

т.к. 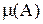в этом случае =0.

Это значит, что точка пересечения этих характеристик должна лежать на одной вертикали. Для того что бы можно было совместить эти характеристики необходимо что бы общее ФЧХ НЭ было построено в координатах 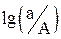, от 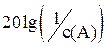. Амплитуда при построении должна расти слева направо. Существуют шаблоны ЛАЧХ и ФЧХ для НЭ, которые приводятся в справочниках.

Для определения параметров автоколебаний строят АФЧХ ЛЧ шаблон с ЛАЧХ смещают по оси абсцисс так, что бы ос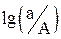и и 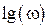совпали (можно перемещать по оси абсцисс). Этот шаблон перемещается, пока не получится совмещение на одной вертикали ФЧХ и АЧХ.

Частоту колебаний определяют по оси абсцисс по АЧХ ЛЧ. Амплитуду определяют по оси абсцисс с графика НЭ.

Если двигаться по графику 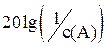в сторону увеличения амплитуды мы выходим из зоны, охваченной АЧХ и осью Х, то режим устойчив.

Если ЛЧ будет неустойчивой, а НЭ имеет ограничение или насыщение, то в большинстве случаев в системе установиться режим незатухающих колебаний с большой амплитудой. Амплитуду их можно посчитать следующим образом:

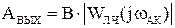
Для того что бы оценить влияние ЛЧ системы на поведение НЭ строят специальные диаграммы качества.