Теорема, устанавливающая необходимое и достаточное условие существования базисного решения системы ограничений, безотносительно к способу их получения

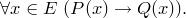
Предикат 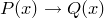является истинным для всех 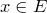тогда и только тогда, когда множество истинности предиката 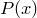содержится в множестве истинности предиката 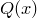, т.е. предикат 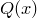является следствием предиката 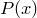. При этом предикат 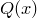называют необходимым условием для предиката 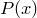, а предикат 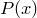— достаточным условием для .

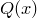Пример. Рассмотрим утверждение: “Если число 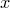делится на 6, то число 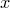делится на 3”. Здесь предикат 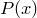: “Число 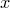делится на 6”, а предикат 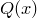: “Число 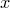делится на 3”. Предикат 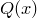логически следует из предиката 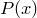. Предикат 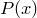(делимость числа 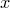на 6) является достаточным условием для предиката 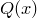(делимость числа 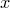на 3). Предикат 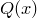(делимость числа 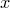на 3) является необходимым условием для предиката 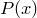(делимость числа 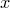на 6).

Часто встречается ситуация, при которой истинны теоремы

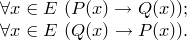
Это возможно при условии, что предикаты 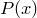и 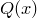равносильны. В таком случае из первой теоремы следует, что условие 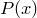является достаточным для 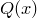, а из второй теоремы следует, что условие 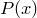является необходимым для 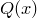. Таким образом, в этом случае условие 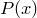является и необходимым, и достаточным условием для 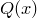. Аналогично, условие 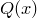является необходимым и достаточным для .

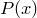Пример. Рассмотрим теоремы: “В описанном четырехугольнике суммы длин противоположных сторон равны” и “Если в четырехугольнике суммы длин противоположных сторон равны, в этот четырехугольник можно вписать окружность”. Обе они истинны. Каждое из условий “В четырехугольнике суммы длин противоположных сторон равны” и “В четырехугольник можно вписать окружность” является и необходимым, и достаточным.