Компактное множество- подмножество Мтопологич. пространства Xтакое, что каждая бесконечная последовательность 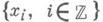 содержит подпоследовательность, сходящуюся к нек-рой точке х 0 пространства X. Если
содержит подпоследовательность, сходящуюся к нек-рой точке х 0 пространства X. Если  то Мназ. компактным в себе множеством. Оно является компактным пространством виндуцированной из Xтопологии. Обратно, всякое К. м. метрич. пространства является в такой топологиикомпактным пространством. Множество, замыкание к-рого - К. м., наз. относительно компактныммножеством. Мажоранта или верхняя грань (граница) числового множества
то Мназ. компактным в себе множеством. Оно является компактным пространством виндуцированной из Xтопологии. Обратно, всякое К. м. метрич. пространства является в такой топологиикомпактным пространством. Множество, замыкание к-рого - К. м., наз. относительно компактныммножеством. Мажоранта или верхняя грань (граница) числового множества 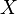 — число
— число 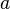 , такое что
, такое что 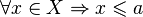 Миноранта или нижняя грань (граница) числового множества
Миноранта или нижняя грань (граница) числового множества 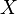 — число
— число 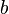 , такое что
, такое что 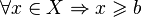 Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества
Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества 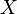 упорядоченного множества (или класса)
упорядоченного множества (или класса) 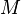 , называется наименьший элемент
, называется наименьший элемент 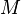 , который равен или больше всех элементов множества
, который равен или больше всех элементов множества 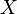 . Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается
. Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается 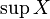 .Более формально:
.Более формально: 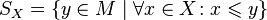 — множество верхних граней
— множество верхних граней 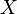 , то есть элементов
, то есть элементов 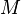 , равных или больших всех элементов
, равных или больших всех элементов 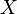
|
|
|
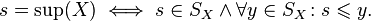 Точной (наибольшей) нижней гранью (границей), или инфи́мумом (лат. infimum — самый низкий) подмножества
Точной (наибольшей) нижней гранью (границей), или инфи́мумом (лат. infimum — самый низкий) подмножества 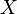 упорядоченного множества (или класса)
упорядоченного множества (или класса) 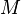 , называется наибольший элемент
, называется наибольший элемент 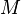 , который равен или меньше всех элементов множества
, который равен или меньше всех элементов множества 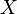 . Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается
. Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается 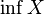 .
.
Эти определения ничего не говорят о том, принадлежит ли 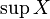 и
и 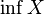 множеству
множеству 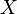 или нет.
или нет.
В случае 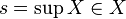 , говорят, что
, говорят, что  является максимумом
является максимумом 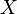 , то есть
, то есть 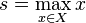 .
.
В случае 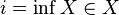 , говорят, что
, говорят, что 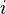 является минимумом
является минимумом 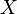 , то есть
, то есть 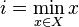
Следует отметить, что приведенные определения точных граней являются непредикативными (ссылающимися на самих себя) определениями, поскольку определяемое понятие в каждом из них является элементом множества, через которое оно определяется (см. подробнее в Impredicativity). Сторонники конструктивизма в математике выступают против использования таких определений, не допуская либо различными методами устраняя элементы "порочного круга" в рамках своих теорий.
Теоре́ма Вейерштра́сса в математическом анализе и общей топологии гласит, что функция, непрерывная на компакте, ограничена на нём и д В частном случае функций действительной переменной (который обычно излагается в учебниках матанализа), теорема формулируется так:
Если функция 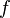 непрерывна на отрезке
непрерывна на отрезке 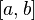 , то она ограничена на нем и притом достигает своих минимального и максимального значений, т.е. существуют
, то она ограничена на нем и притом достигает своих минимального и максимального значений, т.е. существуют 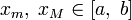 такие, что
такие, что 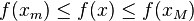 для всех
для всех 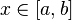
В силу полноты действительных чисел существует (конечная или бесконечная) точная верхняя грань 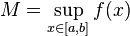 . Поскольку
. Поскольку 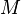 - точная верхняя грань, существует последовательность
- точная верхняя грань, существует последовательность 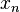 такая, что
такая, что 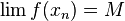 . По теореме Больцано — Вейерштрасса из последовательности
. По теореме Больцано — Вейерштрасса из последовательности 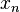 можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность 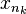 , предел которой (назовем его
, предел которой (назовем его 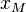 ) также принадлежит отрезку
) также принадлежит отрезку 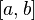 . В силу непрерывности функции
. В силу непрерывности функции 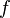 имеем
имеем 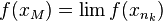 , но с другой стороны
, но с другой стороны 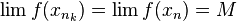 . Таким образом, точная верхняя грань
. Таким образом, точная верхняя грань 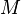 конечна и достигается в точке
конечна и достигается в точке 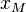 .
.
|
|
|
Для нижней грани доказательство аналогично.
 2015-02-04
2015-02-04 1555
1555








