2015-02-14
752
Получим зависимость для нормального напряжения, которое возникает в поперечных сечениях стержня. Для этого рассмотрим две стороны задачи о растяжении некоторого стержня.
Статическая сторона задачи.
Используем первую зависимость интегрального уравнения равновесия [глава 2, формула (6.4)].
Чтобы получить зависимость для нахождения нормального напряжения s z, необходимо провести анализ напряженно-деформированного состояния стержня, то есть установить закон изменения напряжений по сечению стержня.
Геометрическая сторона задачи.
На основании анализа деформации стержня (смотри изменение сетки на поверхности стержня – рисунок 1.1) показывает, что при растяжении-сжатии является справедливой гипотеза плоских сечений (гипотеза Бернулли) – сечения, плоские до деформации, остаются плоскими и после деформации.
На основании этого можно считать, что деформации и, соответственно, нормальные напряжения по сечению стержня распределяются равномерно или по постоянному закону.
Тогда с учетом (1.2) преобразуем (1.1):
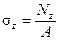 | (1.4)* |
Таким образом, при растяжении-сжатии в поперечных сечениях стержня возникают нормальные напряжения, определяемые отношением продольной силы к площади сечения.
