 Рис. 21.3
Рис. 21.3
|
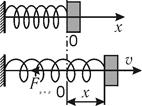
Укрепим на конце пружины тело массой m, которое может свободно (без трения) перемещаться вдоль стержня (рис. 21.3). При смещении тела на величину x от положения равновесия возникает упругая сила (см. § 2.6) F=-kx, которая стремится вернуть тело в положение равновесия. Если отпустить тело, то под действием этой силы оно начнет двигаться.
Для нахождения уравнения движения воспользуемся вторым законом Ньютона:
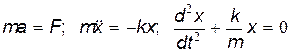 . .
| (21.7) |
Сравнивая (21.6) и (21.7), видим, что пружинный маятник совершает колебания с частотой
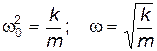 . .
| (21.8) |
Период колебаний пружинного маятника
 Рис. 21.4
Рис. 21.4
|
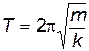 .
.
Следует отметить, что все упруго деформированные тела приходят в колебательное движение, частота которого определяется общей формулой (21.8), однако значения коэффициента упругости (жесткости) каждом конкретном случае различны. Так, упруго колеблются детали судового набора, валы, трубопроводы и т.д.
 2015-02-04
2015-02-04 684
684








