Основные понятия комбинаторики. Комбинаторика–раздел математики, изучающий способы подсчета числа элементов в конечных множествах

Комбинаторика – раздел математики, изучающий способы подсчета числа элементов в конечных множествах.

Пусть .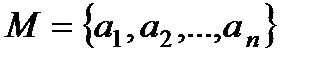

1. Система подмножеств множества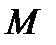

Пример. .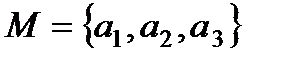

, , , , , , , .●

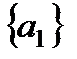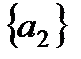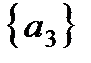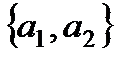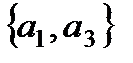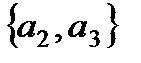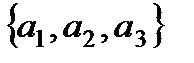Число подмножеств равно .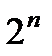

2. Размещение элементов из 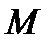по k – упорядоченное подмножество из k элементов, принадлежащих .

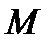Пример. , .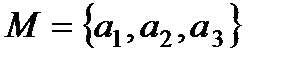

, , , , , .

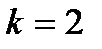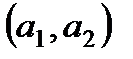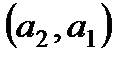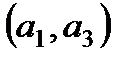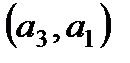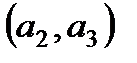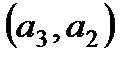Число размещений равно .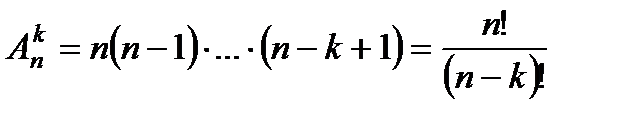

3. Перестановки элементов множества 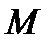– упорядоченные подмножества из п элементов множества .

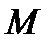Пример. .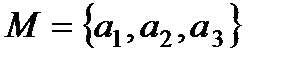

, , , , , .

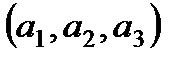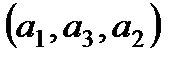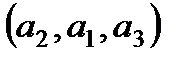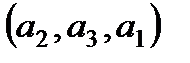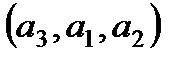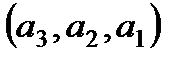Число перестановок равно .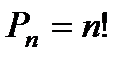

4. Сочетание элементов из 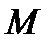по k – неупорядоченное подмножество из k элементов, принадлежащих .

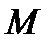Пример. , .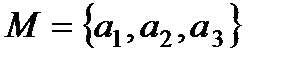

, , .

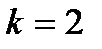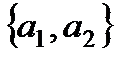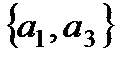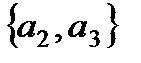Число сочетаний равно .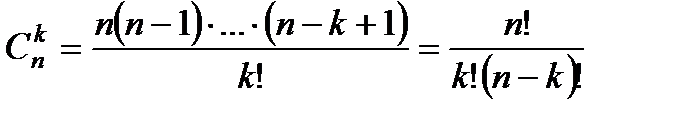

5. Разбиение множества 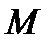– неупорядоченная система из непустых подмножеств 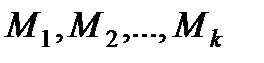множества 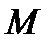, обладающая свойствами:

1) ,

2) .

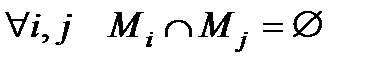Правило произведения. Если объект 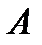может быть выбран 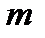способами и после каждого из таких выборов объект 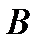, в свою очередь, может быть выбран 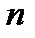способами, то выбор « 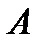и 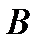» в указанном порядке может быть осуществлен 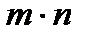способами.

Правило суммы. Если объект 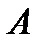может быть выбран 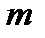способами, а объект 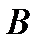– другими 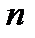способами при условии, что одновременный выбор 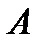и 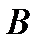невозможен, то выбор « 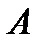или 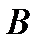» можно осуществить 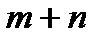способами.