Суммой событий 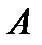 и
и 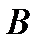 называют событие
называют событие 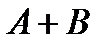 , состоящее в появлении хотя бы одного из событий.
, состоящее в появлении хотя бы одного из событий.
Аналогично определяется сумма нескольких событий.
Теорема. Если 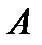 и
и 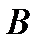 – несовместные события, то
– несовместные события, то
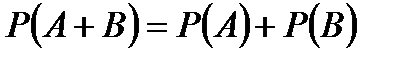 .
.
Следствие. Если 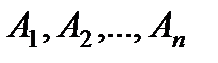 – попарно несовместные события, то
– попарно несовместные события, то
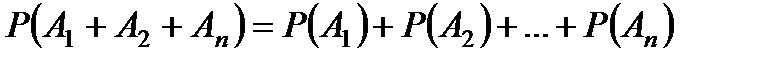 .
.
Пример 1. Среди лотерейных билетов 10 билетов с выигрышем по 100 рублей и 5 билетов с выигрышем по 500 рублей. Какова вероятность выигрыша при покупке одного билета?
Решение. Обозначим события 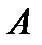 – выигрыш 100 рублей,
– выигрыш 100 рублей, 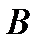 – выигрыш 500 рублей.
– выигрыш 500 рублей.
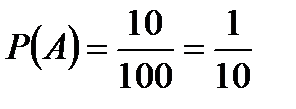 ,
, 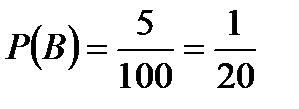 .
.
События 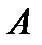 и
и 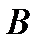 несовместны, поэтому
несовместны, поэтому
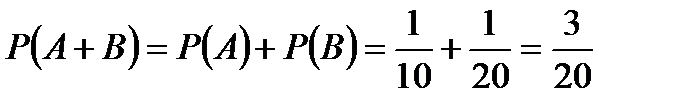 .●
.●
Теорема. Сумма вероятностей попарно несовместных событий 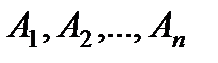 , образующих полную группу, равна 1:
, образующих полную группу, равна 1:
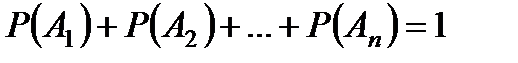 .
.
Определение. Противоположными называют два единственно возможных события, образующих полную группу.
Обозначение: 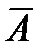 – событие, противоположное событию
– событие, противоположное событию 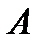 .
.
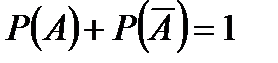 .
.
Пример 2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди двух наудачу извлеченных деталей есть хотя бы одна стандартная.
Решение. Событие 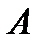 – среди извлеченных деталей есть хотя бы одна стандартная. Тогда событие
– среди извлеченных деталей есть хотя бы одна стандартная. Тогда событие 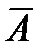 – среди извлеченных деталей нет ни одной стандартной.
– среди извлеченных деталей нет ни одной стандартной.
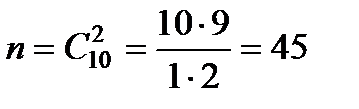 – общее число исходов,
– общее число исходов,
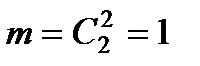 – число исходов благоприятствующих событию
– число исходов благоприятствующих событию 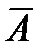 .
.
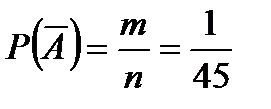 ,
,
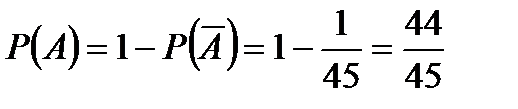 . ●
. ●
 2015-02-14
2015-02-14 1841
1841








