События называются несовместными, если они не могут появиться вместе в одном опыте. Если одно из событий произойдет обязательно, то такие события образуют полную группу.
Суммой событий называется событие, состоящее в появлении хотя бы одного из рассматриваемых событий.
Теорема: Вероятность суммы несовместимых событий равна сумме вероятностей этих событий.
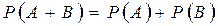 или
или 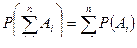
Сумма вероятностей событий, образующих полную группу, равна единице.
Произведением событий называется событие, состоящее в появлении всех из рассматриваемых событий.
Вероятность события 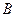 , вычисленная при условии, что произошло событие
, вычисленная при условии, что произошло событие 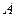 , называется условной вероятностью события
, называется условной вероятностью события 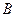 относительно события
относительно события 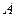 . Эта вероятность обозначается
. Эта вероятность обозначается 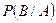 .
.
Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго относительно первого: 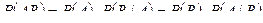 .
.
Эта теорема обобщается на любое конечное число событий.
Если появление одного из событий не влияет на вероятность появления другого, то такие события называются независимыми.
Для независимых событий вероятность их произведения равна произведению вероятностей этих событий. Для двух независимых событий
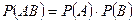 .
.
События называются совместными, если они могут появиться одновременно в одном опыте.
Теорема: Вероятность сложения двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: 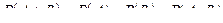 .
.
В некоторых случаях вероятность события удобнее подсчитывать как вероятность противоположного другому событию.
Пусть события 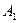 ,
, 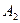 ,...,
,...,  независимы и известны вероятности этих событий:
независимы и известны вероятности этих событий: 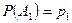 ,
, 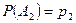 ,...,
,...,  . Обозначив вероятности противоположных событий
. Обозначив вероятности противоположных событий 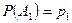 ,
, 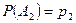 ,...,
,...,  . Обозначив вероятности противоположных событий
. Обозначив вероятности противоположных событий 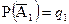 ,
, 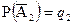 ,...,
,..., 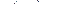 , найдем вероятность того, что ни одно из событий
, найдем вероятность того, что ни одно из событий 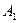 ,
, 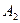 ,...,
,...,  в опыте не наступит:
в опыте не наступит:  ...
...  .
.
В этом случае искомая вероятность, т.е. вероятность появления хотя бы одного события, определяется как вероятность противоположного события

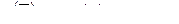 ...
...  .
.
Если некоторое событие 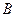 совершается с одним из
совершается с одним из 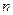 несовместимых событий
несовместимых событий 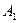 ,
, 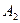 ,...,
,...,  , образующих полную группу событий, то для определения вероятности этого события может быть использована формула полной вероятности
, образующих полную группу событий, то для определения вероятности этого события может быть использована формула полной вероятности
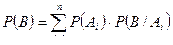 ,
,
где  – вероятность события
– вероятность события  ,
, 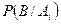 – условная вероятность события
– условная вероятность события 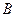 .
.
Для определения вероятности события  при условии, что произошло событие
при условии, что произошло событие 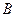 , используется формула Байеса
, используется формула Байеса 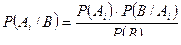 . Если при проведении испытаний вероятность появления события
. Если при проведении испытаний вероятность появления события 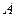 не зависит от исходов других испытаний, то такие испытания называются независимыми.
не зависит от исходов других испытаний, то такие испытания называются независимыми.
Формула Бернулли определяет вероятность появления ровно 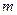 раз события
раз события 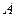 в серии из
в серии из 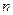 – независимых испытаний, в каждом из которых вероятность появления события
– независимых испытаний, в каждом из которых вероятность появления события 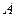 равна
равна 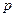 :
:
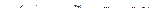 , где
, где 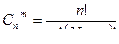 ,
, 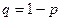 .
.
В ряде случаев требуется определитель вероятности появления события 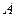 менее
менее 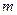 раз
раз 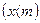 , более
, более 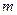 раз
раз 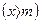 , не менее
, не менее 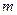 раз
раз 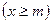 , не более
, не более 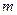 раз
раз 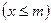 . В этих случаях могут быть использованы формулы
. В этих случаях могут быть использованы формулы
 ,
,
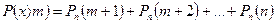 ,
,
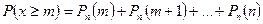 ,
,
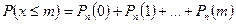 .
.
При больших 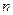 и малых
и малых 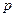 вычисления по формуле Бернулли затруднены. В этих случаях обычно используется формула Пуассона
вычисления по формуле Бернулли затруднены. В этих случаях обычно используется формула Пуассона
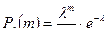 ,
, 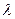 – пр.
– пр.
Задача 1. В партии из 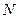 деталей имеется
деталей имеется 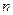 стандартных. Наудачу отобраны
стандартных. Наудачу отобраны 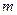 деталей. Найти вероятность того, что среди отобранных деталей ровно
деталей. Найти вероятность того, что среди отобранных деталей ровно 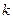 стандартных.
стандартных.
Решение:
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 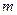 деталей из
деталей из 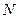 деталей, т.е.
деталей, т.е.  – числу сочетаний из
– числу сочетаний из 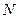 элементов по
элементов по 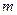 .
.
Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди 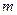 деталей ровно
деталей ровно 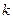 стандартных):
стандартных): 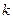 стандартных деталей можно взять из
стандартных деталей можно взять из 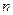 стандартных деталей
стандартных деталей 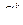 способами; при этом остальные
способами; при этом остальные 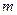 –
– 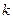 деталей должны быть нестандартными; взять же
деталей должны быть нестандартными; взять же 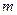 –
– 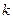 нестандартных деталей из
нестандартных деталей из 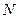 –
– 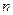 нестандартных деталей можно
нестандартных деталей можно  способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно
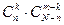 .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
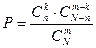 .
.
Задача 2. Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин приобрел по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов.
Решение:
Общее число элементарных исходов равно 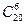 . Число благоприятствующих исходов определяется как произведение
. Число благоприятствующих исходов определяется как произведение 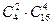 , где
, где 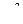 – число способов выбора АО – банкротов из четырех. Но с каждым способом такого выбора могут встретиться АО, не являющиеся банкротами. Таких будет
– число способов выбора АО – банкротов из четырех. Но с каждым способом такого выбора могут встретиться АО, не являющиеся банкротами. Таких будет 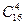 . Искомая вероятность равна
. Искомая вероятность равна 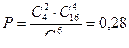
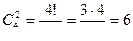 ;
;
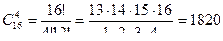 ;
;
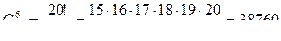 ;
;
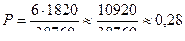 .
.
Задача 3. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие 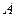 ).
).
Решение:
I способ. Условие – хотя бы один из трех взятых учебников в переплете будет осуществлено, если произойдет любое из следующих трех несовместных событий: 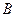 – один учебник в переплете,
– один учебник в переплете,
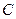 – два учебника в переплете,
– два учебника в переплете,
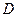 – три учебника в переплете.
– три учебника в переплете.
Интересующее нас событие 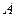 можно представить в виде суммы событий:
можно представить в виде суммы событий:
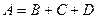 . По теореме сложения,
. По теореме сложения, 
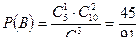 ;
; 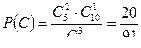 ;
; 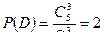 ;
;
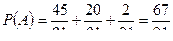
II способ. События 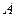 (хотя бы один из взятых трех учебников имеет переплет) и
(хотя бы один из взятых трех учебников имеет переплет) и 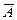 (ни один из взятых учебников не имеет переплета) – противоположные, поэтому
(ни один из взятых учебников не имеет переплета) – противоположные, поэтому 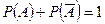 (сумма вероятностей двух противоположных событий равна единице. Отсюда
(сумма вероятностей двух противоположных событий равна единице. Отсюда 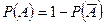 . Вероятность появления события
. Вероятность появления события 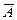 (ни один из взятых учебников не имеет переплета)
(ни один из взятых учебников не имеет переплета) 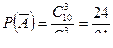 . Искомая вероятность
. Искомая вероятность 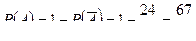 .
.
Задача 4. Вероятности появления каждого из двух независимых событий 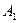 и
и 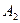 соответственно равны
соответственно равны 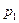 и
и 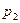 . Найти вероятность появления только одного из этих событий.
. Найти вероятность появления только одного из этих событий.
Решение:
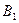 – появилось только событие
– появилось только событие 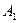 ;
;
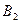 – появилось только событие
– появилось только событие 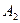 .
.
Появление события 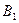 равносильно появлению события
равносильно появлению события 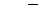 появилось первое событие и не появилось второе, т.е.
появилось первое событие и не появилось второе, т.е. 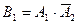 . Появление события
. Появление события 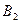 равносильно появлению события
равносильно появлению события 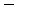 (появилось второе событие и не появилось первое, т.е.
(появилось второе событие и не появилось первое, т.е.  . Таким образом, чтобы найти вероятность появления только одного из событий
. Таким образом, чтобы найти вероятность появления только одного из событий 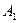 и
и 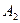 , достаточно найти вероятность появления одного, безразлично какого из событий
, достаточно найти вероятность появления одного, безразлично какого из событий 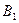 и
и 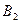 . События
. События 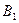 и
и 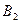 не совместимы, поэтому применима теорема сложения:
не совместимы, поэтому применима теорема сложения:
 .
.
Остается найти вероятности каждого из событий 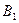 и
и 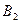 . События
. События 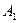 и
и 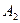 независимы, следовательно, независимы события
независимы, следовательно, независимы события 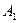 и
и  , а также
, а также 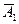 и
и 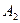 , поэтому применима теорема умножения:
, поэтому применима теорема умножения:
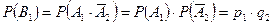 ;
;
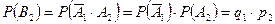 .
.
Подставив эти вероятности, найдем искомую вероятность появления только одного из 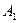 и
и 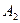 :
:
 .
.
Задача 5. В цехе работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение:
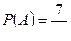
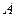 – первым отобран мужчина;
– первым отобран мужчина;
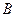 – вторым отобран мужчина. Вероятность того, что вторым отобран мужчина, при условии, что первым уже был мужчина, т.е. условная вероятность события
– вторым отобран мужчина. Вероятность того, что вторым отобран мужчина, при условии, что первым уже был мужчина, т.е. условная вероятность события 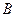 следующая:
следующая: 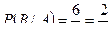
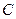 – третьим отобран мужчина.
– третьим отобран мужчина.
Вероятность того, что третьим будет отобран мужчина, при условии, что уже отобраны двое мужчин, т.е. условная вероятность события 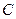 такова:
такова: 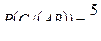 . Искомая вероятность того, что все три отобранных лица окажутся мужчинами,
. Искомая вероятность того, что все три отобранных лица окажутся мужчинами, 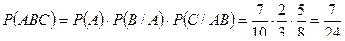 .
.
Задача 6. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны 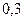 ;
; 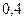 ;
; 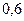 ;
; 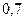 .
.
Решение:
Мост будет разрушен (событие 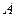 ), если хотя бы одна бомба попадет в цель.
), если хотя бы одна бомба попадет в цель.
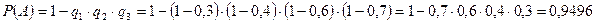 .
.
Задача 7. На автозавод поступили двигатели трёх моторных заводов. От первого завода поступило 10 двигателей, от второго – 6 двигателей и от третьего – 4 двигателя. Вероятности безотказной работы этих двигателей в течение гарантийного срока соответственно равны 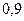 ;
; 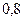 ;
; 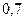 . Найти вероятность того, что: а) установленный на машине двигатель будет работать без дефектов в течение гарантийного срока;б) проработавший без дефекта двигатель изготовлен на первом заводе, на втором заводе?
. Найти вероятность того, что: а) установленный на машине двигатель будет работать без дефектов в течение гарантийного срока;б) проработавший без дефекта двигатель изготовлен на первом заводе, на втором заводе?
Решение:
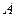 – наугад взятый двигатель проработает без дефектов;
– наугад взятый двигатель проработает без дефектов;
Можно выдвинуть три гипотезы:
 – двигатель изготовлен на первом заводе;
– двигатель изготовлен на первом заводе;
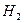 – двигатель изготовлен на втором заводе;
– двигатель изготовлен на втором заводе;
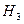 – двигатель изготовлен на третьем заводе.
– двигатель изготовлен на третьем заводе.
Вероятности этих гипотез таковы: 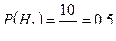 ;
; 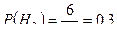 ;
;  . Вероятность того, что наугад взятый двигатель проработает без дефектов, найдем по формуле полной вероятности:
. Вероятность того, что наугад взятый двигатель проработает без дефектов, найдем по формуле полной вероятности:
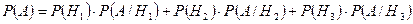 .
.
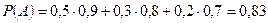 .
.
б) Если двигатель проработал без дефектов гарантийный срок, то вероятности того, что он изготовлен на первом, на втором заводах, найдём по формуле Байеса:
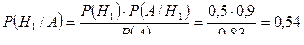 ,
,
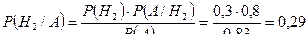 .
.
Задача 8. Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется холодильник марки « » равна
» равна 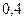 . Найти вероятность того, что холодильник потребуется:
. Найти вероятность того, что холодильник потребуется:
а) не менее чем двум покупателям;
б) не более чем трем покупателям;
в) всем четырем покупателям.
Решение:
а) не менее чем двум покупателям, – это означает, что потребуется двум покупателям, или трем или четырем.
Выясним эту вероятность, используя формулу Бернулли:
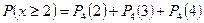 ;
;
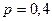 ;
; 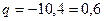 ;
; 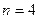
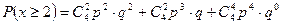 ;
;
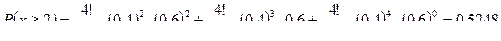 .
.
б) вероятность того, что холодильник потребуется не более чем трём покупателям означает, что никому не потребуется или одному покупателю, или двум. или трём, т.е.
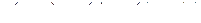 ;
;
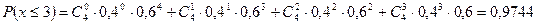 ;
;
в) вероятность того, что холодильник потребуется всем четырём покупателям, т.е.
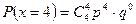
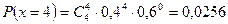 .
.
Случайные величины
Закон распределения вероятностей дискретной
случайной величины.
Определение: Случайной величинойназывается величина, которая в результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.
Определение: Дискретной случайной величинойназывается такая, значения которой есть конечное или счетное множество фиксированных величин. Для описания поведения дискретной случайной величины  задают все значения
задают все значения 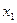 ,
, 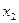 ,
, 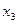 , …,
, …, 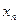 , которые она может принять, и вероятности появления этих значений
, которые она может принять, и вероятности появления этих значений 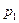 ,
, 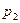 ,
,  , …,
, …,  .
.
Определение: Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, причем 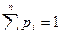 :
:
 | 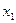 | 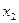 | ... | 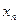 |
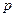 | 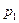 | 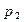 | ... |  |
Ряд распределения можно задать графически, откладывая на горизонтальной оси значения 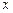 , а на вертикальной – соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.
, а на вертикальной – соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.
Для дискретной случайной величины можно ввести понятие функции распределения 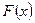 , которая равна вероятности случайного события, состоящего в том, что ДСВ
, которая равна вероятности случайного события, состоящего в том, что ДСВ 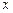 примет одно из возможных значений, меньших некоторого значения
примет одно из возможных значений, меньших некоторого значения 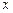 , т.е.
, т.е. 
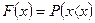 .
.
Если дискретные значения случайной величины расположены в порядке возрастания 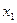 ,
, 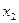 ,
, 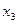 , …,
, …, 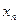 , то
, то 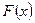 можно задать в виде
можно задать в виде
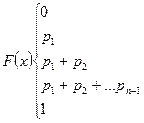
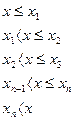
Функцию распределения можно представить графически в виде ступенчатой функции

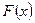
 | |||||||
 |  |  | |||||



Определение: Биноминальным называют закон распределения ДСВ 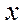 – числа появления события в
– числа появления события в 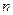 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна 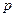 ; вероятность возможного значения
; вероятность возможного значения 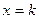 (числа
(числа 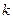 появлений события) вычисляют по формуле Бернулли:
появлений события) вычисляют по формуле Бернулли:
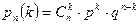
Если число испытаний велико, а вероятность 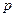 появления события в каждом испытании очень мала, то используют приближенную формулу
появления события в каждом испытании очень мала, то используют приближенную формулу

 ,
,
где 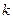 – число появлений события в
– число появлений события в 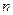 независимых испытаниях,
независимых испытаниях, 
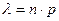 , и говорят, что случайная величина распределена по закону Пуассона. Закон распределения Пуассона является предельным случаем биноминального распределения, его часто еще называют «законом редких чисел», т.к.
, и говорят, что случайная величина распределена по закону Пуассона. Закон распределения Пуассона является предельным случаем биноминального распределения, его часто еще называют «законом редких чисел», т.к. 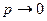 ,
, 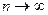 ,
, 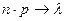 . Обычно для его применения достаточно
. Обычно для его применения достаточно 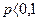 ;
; 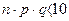 .
.
Задача 9. Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0,7. Построить ряд распределения числа попаданий мяча в корзину.
Решение:
Пусть  – случайная величина числа попаданий мяча в корзину. Баскетболист может не попасть ни разу, один раз, два раза и все три раза,
– случайная величина числа попаданий мяча в корзину. Баскетболист может не попасть ни разу, один раз, два раза и все три раза,
т.е.  ,
, 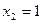 ,
,  ,
,  . Вероятности вычисляем по формуле Бернулли,
. Вероятности вычисляем по формуле Бернулли,
при этом 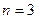 ;
; 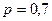 ;
; 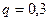

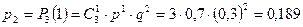
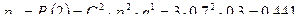
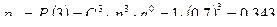
Проверим выполнение 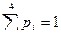 .
.
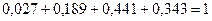
Ряд распределения случайной величины числа попаданий мяча в корзину при трех бросках имеет вид
 | 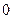 | 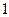 |  | 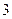 |
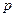 | 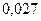 | 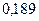 | 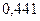 | 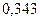 |
Составим функцию распределения 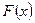 :
:
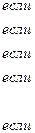
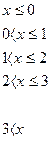
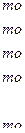
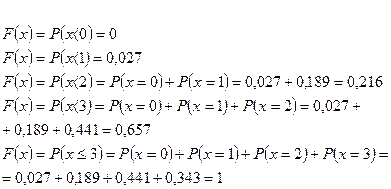
Построим функцию распределения
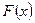
 | |||||
 | |||||
| |||||
|

 | |||
 | |||
|

|
 |  | ||||
 | |||||

|
|
|
|
х
Задача 10. В партии из 25 кожаных курток пять имеют скрытый дефект. Покупают три куртки. Найти закон распределения числа дефектных курток среди купленных. Построить многоугольник распределения.
Решение:
Пусть  – случайная величина числа дефектных курток среди купленных, она может принимать значения:
– случайная величина числа дефектных курток среди купленных, она может принимать значения: 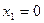 ,
, 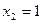 ,
,  ,
, 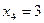 . Для определения вероятности появления каждого из этих значений воспользуемся формулой:
. Для определения вероятности появления каждого из этих значений воспользуемся формулой:
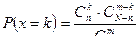 ,
,
где 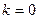 ;
; 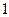 ;
;  ;
; 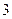 – число дефектных курток,
– число дефектных курток, 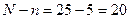 – курток без дефекта;
– курток без дефекта; 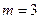 .
.
Вычисляем соответствующие вероятности:
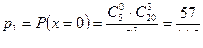 ;
; 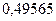
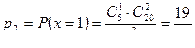 ;
; 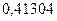
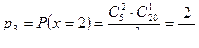 ;
; 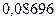
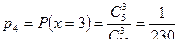 ;
; 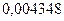
Проверим условие 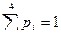 , т.е.
, т.е.
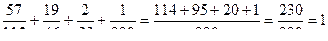 .
.
Построим многоугольник распределения.


 | |||
 | |||
|
|

|

|

|
|

 | |||
 | |||

|
|
|




|
|

 |  |  |  |
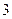 | ||
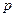 | 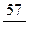 | 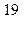 |  | 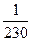 |
Задача 11. Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение:
По условию, 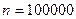 ,
, 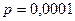 ,
, 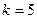 . События, состоящие в том, что книги сброшюрованы неправильно, независимы, число
. События, состоящие в том, что книги сброшюрованы неправильно, независимы, число 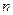 велико, а вероятность
велико, а вероятность 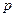 мала, поэтому воспользуемся распределением Пуассона
мала, поэтому воспользуемся распределением Пуассона 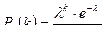 . Найдём
. Найдём 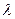 :
: 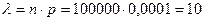 .
.
Искомая вероятность 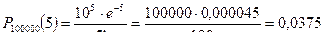 .
.
 2020-10-12
2020-10-12 1300
1300
