| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Решение.
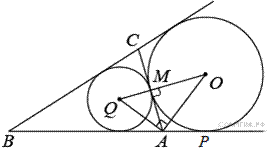 Введём обозначения, приведённые на рисунке. Лучи
Введём обозначения, приведённые на рисунке. Лучи 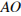 и
и 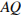 — соответственно биссектрисы углов
— соответственно биссектрисы углов 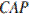 и
и 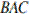 , поскольку эти лучи проходят через центры вписанных окружностей.
, поскольку эти лучи проходят через центры вписанных окружностей. 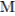 — середина основания
— середина основания 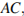 следовательно
следовательно 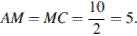 Углы
Углы 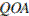 и
и 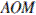 равны друг другу, как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники
равны друг другу, как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники 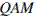 и
и 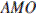 — они прямоугольные и имеют равные углы
— они прямоугольные и имеют равные углы 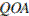 и
и 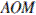 , следовательно эти треугольники подобны:
, следовательно эти треугольники подобны:
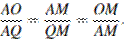
Отсюда следует, что радиус вписаной окружности:
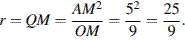
Ответ: 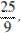
Ваша оценка (баллов): — 0 1 2 3 4
 2015-02-14
2015-02-14 298
298







