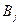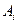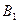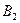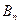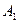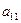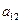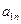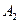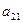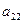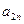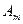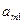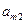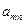Платежная матрица

Составим платежную матрицу для следующей игры.

Игра «Поиск»: Игрок A может спрятаться в одном из двух мест (I и II). Игрок B ищет игрока A, и если найдет, то получает штраф 1 ден. ед. от игрока A, в противном случае платит сам игроку A 1 ден. ед.

Решение. Для составления платежной матрицы проанализируем поведение каждого из игроков. Игрок A может спрятаться в I месте – обозначим эту стратегию 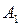, или во II месте – стратегия .

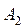Игрок B может искать первого игрока в I месте – стратегия 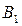, либо во II месте – стратегия .

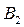Если игрок A находится в I месте и там его обнаруживает игрок B, т.е. осуществляется пара стратегий 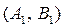, то игрок A платит штраф, т.е. 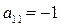. Аналогично получаем 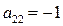для пары стратегий .

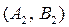Стратеги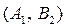и и 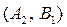дают игроку A выигрыш, т.е. .

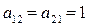Платежная матрица для игры «поиск» размера 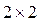будет иметь следующий вид:

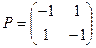Рассмотрим игру 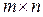с матрицей 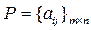и определим наилучшую среди стратегий A₁, A₂, …, A_m. Выбирая стратегию 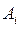игрок A должен рассчитывать, что игрок B ответит на нее той из стратегий 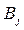, для которой выигрыш игрока A минимален.

Обозначим через 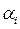наименьший выигрыш игрока A при выборе им стратегии 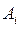для всех возможных стратегий игрока B:

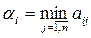. (7.1)

Среди всех 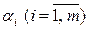выберем наибольшее:

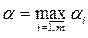. (7.2)

Величину α назовем нижней ценой игры или максиминным выигрышем (максимином). Это гарантированный выигрыш игрока A при любой стратегии игрока B, т.е.:

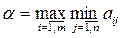. (7.3)

Стратегия, соответствующая максимину, будем называть максиминной стратегией.

Игрок B, в свою очередь, заинтересован в том, чтобы уменьшить выигрыш игрока A: выбирая стратегию B_j, он учитывает максимально возможный при этом выигрыш для игрока A. Обозначим

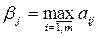. (7.4)

Среди всех β_j выберем наименьшее:

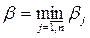. (7.5)

Величину β назовем верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока B, т.е.:

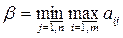. (7.6)

Стратегию, соответствующую минимаксу, будем называть минимаксной стратегией.

Принцип, диктующий игрокам выбор наиболее «осторожных» минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип вытекает из разумного предположения, что каждый игрок стремиться достичь цели, противоположной цели противника.

Определим нижнюю и верхнюю цены «поиск».

При выборе стратегии А₁ минимальный выигрыш равен 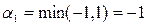и соответствует стратегии В₁ игрока В. При выборе стратегии А₂ минимальный выигрыш равен 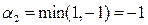и достигается при стратегии В₂.

Гарантируя себе максимальный выигрыш при любой стратегии игрока B, т.е. нижнюю цену игры 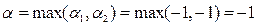. Игрок A может выбирать любую стратегию: А₁ или А₂, т.е. любая его стратегия является максиминной.

Выбирая стратегию B₁, игрок B понимает, что игрок А ответит стратегией A₂, чтобы максимизировать свой выигрыш. Следовательно, максимальный проигрыш игрока B при выборе им стратегии B₁ равен: .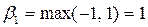

Аналогично максимальный проигрыш игрока B при выборе им стратегии B₂ равен: .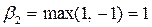

Таким образом, при любой стратегии игрока A гарантированный минимальный проигрыш игрока B (верхняя цена игры) равен: 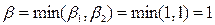. Любая стратегия игрока B является минимаксной.