Если при 
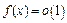 , а
, а 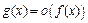 , то говорят, что функция
, то говорят, что функция 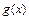 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 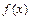 при
при  .
.
Пример 4. Установить, какие из следующих утверждений верны:
1) 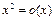 при а)
при а)  , б)
, б) 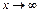 ;
; 
2) 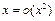 при а)
при а)  , б)
, б) 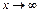 ;
;
3) 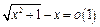 при а)
при а) 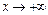 , б)
, б) 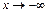 ;
;
4) 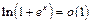 при а)
при а) 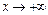 , б)
, б) 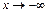 .
.
1) а) Утверждение верно, так как 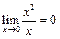 ;
;
б) Утверждение неверно, ибо 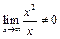 .
.
2) а) Утверждение неверно, так как 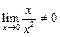 ;
;
б) Утверждение истинно, ибо 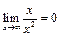 .
.
3) а) Утверждение верно, так как 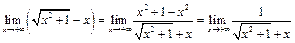
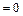 ;
;
б) Утверждение неверно, ибо 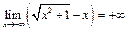 .
.
4) а) Утверждение неверно, так как 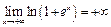 ;
;
б) Утверждение истинно, так как 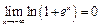 .
.
Пример 5. Доказать или опровергнуть утверждение: 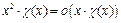 ,
,  , где
, где 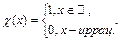
Здесь функция 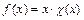 обращается в нуль в точках, сколь угодно близких к точке
обращается в нуль в точках, сколь угодно близких к точке 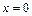 . Поэтому придется воспользоваться определением символа
. Поэтому придется воспользоваться определением символа 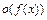 . Так как существует функция
. Так как существует функция 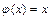 , что
, что 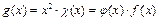 и
и 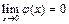 , то
, то 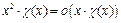 ,
,  - утверждение истинно.
- утверждение истинно.
Замечание!!
При использовании равенств с символами 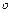 и
и 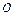 следует иметь в виду, что эти равенства не являются равенствами в обычном смысле. Так, из равенств
следует иметь в виду, что эти равенства не являются равенствами в обычном смысле. Так, из равенств 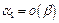 ,
, 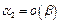 при
при  не следует, что
не следует, что 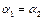 :
: 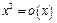 ,
, 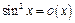 при
при  , но
, но 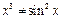 .
.
Пример 6. Докажем следующие правила: при  :
:
1) 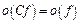 ,
, 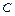 — постоянная;
— постоянная;
2) 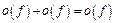 ;
;
3) 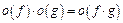 ;
;
4) 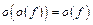 .
.
Для доказательства этих правил возьмем левую часть рассматриваемых равенств и докажем, что ее можно заменить правой.
1) По определению символа 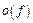 :
:
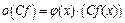 ,
, 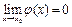 , но тогда
, но тогда
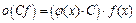 , где
, где 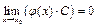 и
и 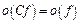 ,
,  .
.
2) Так как 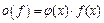 ,
, 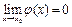 , то
, то 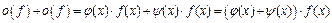 , где
, где 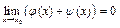 , и, таким образом,
, и, таким образом, 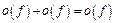 при
при  .
.
3) Учитывая, что 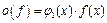 ,
, 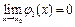 ,
, 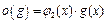 ,
, 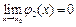 , получим:
, получим: 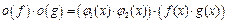 ,
,
где 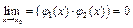 , поэтому:
, поэтому: 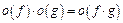 при
при  .
.
4) Так как 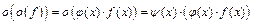 , где
, где 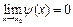 и
и 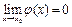 , то
, то 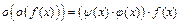 , где
, где 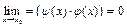 , т.е.
, т.е. 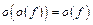 при
при  .
.
В силу доказанных соотношений 1) – 4) левую часть каждого из них можно заменить правой, проделать обратную замену, вообще говоря, нельзя.
Пример 7. Доказать равенства при  :
:
1) 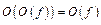 ;
;
2) 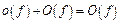 .
.
Обозначим 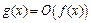 ,согласно определению символа
,согласно определению символа 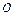 :
: 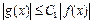 в некоторой
в некоторой 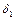 - окрестности точки
- окрестности точки 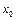 .
.
1) Тогда 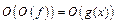 и, вводя обозначение
и, вводя обозначение 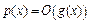 , будем иметь:
, будем иметь: 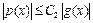 в некоторой
в некоторой
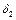 -окрестности точки
-окрестности точки 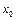 .
.
Если 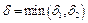 , то в
, то в 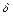 - окрестности точки
- окрестности точки 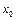 будем иметь
будем иметь 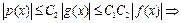
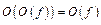 при
при  .
.
2) Символ 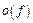 по определению означает:
по определению означает: 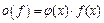 ,
, 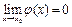 . Тогда
. Тогда 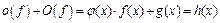 .
.
Так как 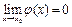 , то в некоторой окрестности точки
, то в некоторой окрестности точки 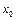
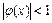 ,следовательно:
,следовательно: 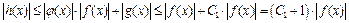 , то есть
, то есть 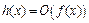 или
или 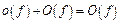 при
при  .
.
Вычисление пределов функций существенно упрощается, если использовать понятие эквивалентности функций и следующие две теоремы.
Теорема 1.
Для того чтобы функции 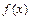 и
и 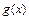 , отличные от нуля в некоторой окрестности точки
, отличные от нуля в некоторой окрестности точки 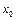 , были эквивалентными при
, были эквивалентными при  , необходимо и достаточно, чтобы выполнялось хотя бы одно из условий:
, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий: 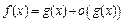 либо
либо 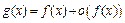 при
при  .
.
Теорема 2.
Пусть 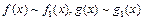 при
при  . Тогда, если существует
. Тогда, если существует 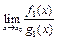 , то существует и
, то существует и 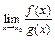 , причем эти пределы равны.
, причем эти пределы равны.
Пример 8.Найти 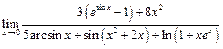 .
.
При  имеем:
имеем: 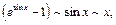
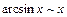 ,
, 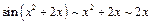 ,
, 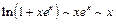 .
.
Следовательно, 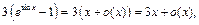
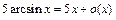 ,
, 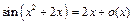 ,
, 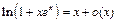 ,и
,и 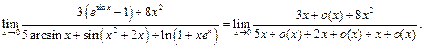 Используя далее правила обращения с символами
Используя далее правила обращения с символами 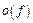 :
: 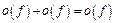 ,
, 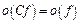
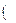 пример 6 (1,2)
пример 6 (1,2) 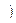 , получим:
, получим:
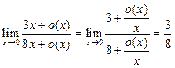 .
.
Пример 9.Найти 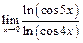 .
.
При  имеем:
имеем: 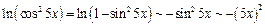 ,
,
аналогично 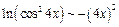 , поэтому
, поэтому 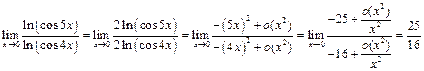 Пример 10. Найти
Пример 10. Найти 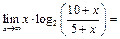
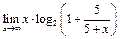 .
.
При 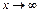 функция
функция 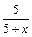
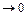 . Тогда, используя замечательный предел
. Тогда, используя замечательный предел 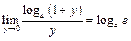 , получим:
, получим: 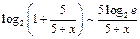 при
при 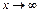 , т.е.
, т.е. 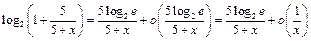 и
и 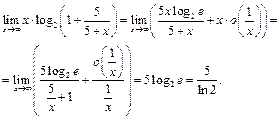
Убедимся, что 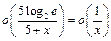 при
при 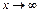 .
.
По определению символа 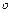 :
: 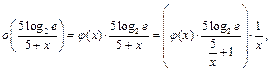 где
где 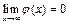 . Но тогда
. Но тогда 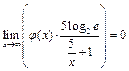 и требуемое установлено.
и требуемое установлено.
Пример 11.Найти 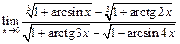 .
.
Воспользуемся замечательным пределом: 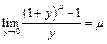 .
.
Тогда 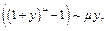
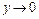 .
.
Поэтому 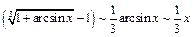 ,
, 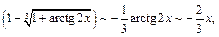
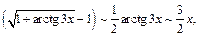
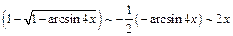 при
при  .
.
Следовательно, 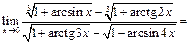
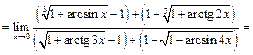
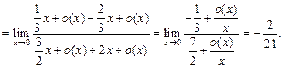
 2015-02-14
2015-02-14 244
244








