2015-02-14
278
Функция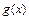 
называется бесконечно малой по сравнению с функцией 
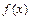при 
, если в некоторой проколотой окрестности точки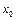 
существует такая функция 
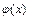, что 
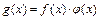и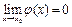 
.
Из определения следует, что если в окрестности точки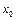 
, 
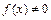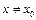, то функция 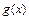будет бесконечно малой по сравнению с 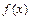при тогда и только тогда, когда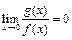 
.
Для обозначения введенного понятия используется запись: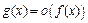 
, (читается так: «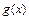 есть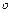 
малое от 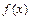при »). Аналогично определяется смысл записи 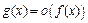при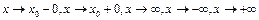 
.
Если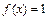 
, то запись 
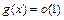при означает, что функция 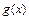является бесконечно малой при .
