Для того чтобы функции 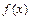 и
и 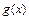 были эквивалентны при
были эквивалентны при  , достаточно, чтобы
, достаточно, чтобы 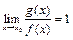 .
.
Из теоремы и известных пределов следуют часто применяемые эквивалентности: 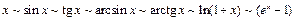 при
при  .
.
Справедливы и более общие эквивалентности: если при 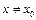 функция
функция 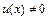 и при
и при 
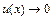 , то при
, то при 
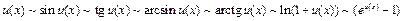 (следует из теоремы о пределе композиции).
(следует из теоремы о пределе композиции).
Пример 3. Какие из следующих пар функций являются эквивалентными при x→ 0:
1) 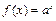 ,
, 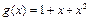 ;
;
2) 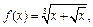
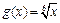 ;
;
3) 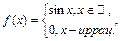
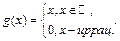
1) Так как 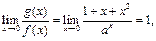 то
то 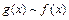 при
при  .
.
2) Так как 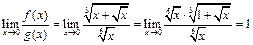 ,
,
то 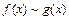 при
при  .
.
3) В этом случае 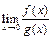 не существует, однако
не существует, однако 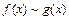 при x→ 0. Действительно, существует функция
при x→ 0. Действительно, существует функция 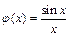 такая, что
такая, что 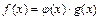 и
и 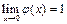 .
.
Теорема дает достаточное условие, но не необходимое. Это условие 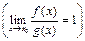 будет являться и необходимым, если в окрестности точки
будет являться и необходимым, если в окрестности точки 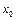
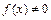 , и
, и 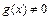 .
.
 2015-02-14
2015-02-14 611
611








