Нахождение для данной функции 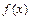 эквивалентной ей при
эквивалентной ей при 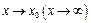 простейшей б.м. или б.б. называется выделением главной части функции при
простейшей б.м. или б.б. называется выделением главной части функции при 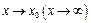 .
.
Пример 12. Выделить главную часть следующих б.м. или б.б. при  функций:
функций:
1) 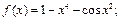 2)
2) 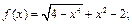
3) 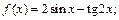 4)
4) 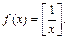
1) Так как 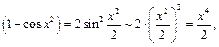 то
то
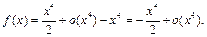
Итак, 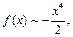
 .
. 
2) Так как 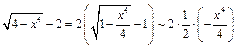 при
при  , то
, то 
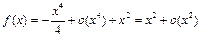 , следовательно,
, следовательно, 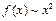 при
при  .
.
3) Требуется найти функцию вида 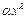 такую, что
такую, что 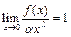 . Рассмотрим
. Рассмотрим 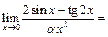
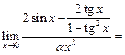
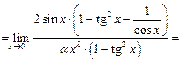
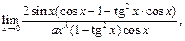
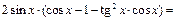
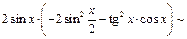 ~
~ 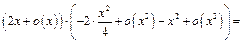
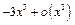 - согласно правилам обращения с символом
- согласно правилам обращения с символом 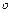 .
.
Тогда 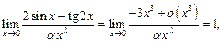 если
если 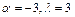 . Следовательно,
. Следовательно, 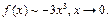
4) Функция 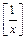 при
при  является бесконечно большой. Эквивалентная ей простейшая б.б. имеет вид:
является бесконечно большой. Эквивалентная ей простейшая б.б. имеет вид: 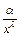 . Для определения вещественных постоянных
. Для определения вещественных постоянных 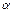 и
и 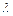 сделаем замену переменной:
сделаем замену переменной: 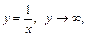 когда
когда  . Любое вещественное
. Любое вещественное 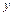 может быть представлено в виде:
может быть представлено в виде: 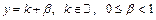 и
и 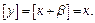 Тогда очевидно, что
Тогда очевидно, что 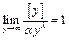 только тогда, когда
только тогда, когда 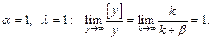
Следовательно, 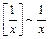 при
при  .
.
 2015-02-14
2015-02-14 280
280








