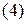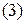Определение. Функция  называется ограниченной на некотором множестве
называется ограниченной на некотором множестве 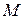 , если для любого
, если для любого 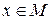 выполняется неравенство
выполняется неравенство 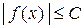 , где
, где 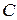 – некоторая положительная константа.
– некоторая положительная константа.
Теорема 1. Пусть функция  имеет предел в точке
имеет предел в точке  , тогда существует проколотая окрестность
, тогда существует проколотая окрестность 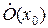 , в которой функция
, в которой функция  ограничена.
ограничена.
Доказательство. Пусть 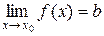 . Это значит, что для любого
. Это значит, что для любого 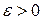 и для
и для 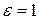 существует
существует 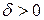 такое, что для любого
такое, что для любого 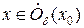 выполняется неравенство
выполняется неравенство 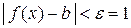 , т.е.
, т.е. 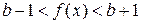 .
.
 Пусть
Пусть 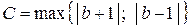 . Тогда для любого
. Тогда для любого 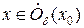 выполняется неравенство
выполняется неравенство 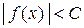 , что и требовалось доказать.
, что и требовалось доказать.
Теорема 2. Если функция  имеет предел при
имеет предел при  , то этот предел единственный.
, то этот предел единственный.
Доказательство. Предположим, что функция  при
при  имеет два различных предела, т.е.
имеет два различных предела, т.е. 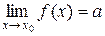 и
и 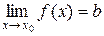 .
.
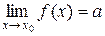 , следовательно:
, следовательно:
для любого 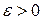 существует
существует 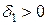 такое, что для любого
такое, что для любого  :
: 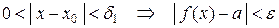 . (1)
. (1)
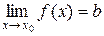 , следовательно:
, следовательно:
для любого 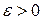 существует
существует 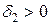 такое, что для любого
такое, что для любого  :
: 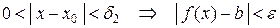 . (2)
. (2)
Пусть 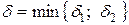 . Тогда для любого
. Тогда для любого  :
: 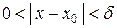 будут одновременно выполняться и неравенство (1), и неравенство (2).
будут одновременно выполняться и неравенство (1), и неравенство (2).
Для этих значений  имеем:
имеем:
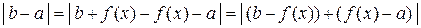 .
.
По свойству модулей имеем:
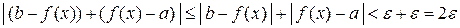 .
.
 Следовательно,
Следовательно, 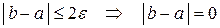 , т.е.
, т.е. 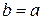 . Следовательно, если предел у функции существует, то он единственный.
. Следовательно, если предел у функции существует, то он единственный.
Теорема 3 (теорема о двух милиционерах). Пусть даны три функции  ,
, 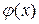 ,
, 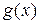 , которые определены в некоторой окрестности
, которые определены в некоторой окрестности 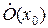 и удовлетворяют условию
и удовлетворяют условию 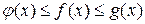 в этой окрестности. Тогда, если
в этой окрестности. Тогда, если 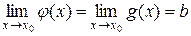 , то
, то 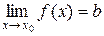 .
.
Доказательство. Пусть  удовлетворяет условию
удовлетворяет условию 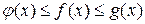 . (*)
. (*)
Пусть 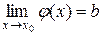 , следовательно:
, следовательно:
для любого 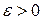 существует
существует 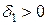 такое, что для любого
такое, что для любого  :
: 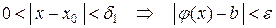 . (3)
. (3)
Пусть 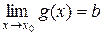 , следовательно:
, следовательно:
для любого 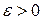 существует
существует 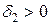 такое, что для любого
такое, что для любого  :
: 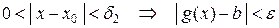 . (4)
. (4)
Пусть 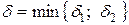 . Тогда для любого
. Тогда для любого  , удовлетворяющего соотношению
, удовлетворяющего соотношению 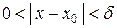 , будут одновременно выполняться и неравенство (3) и неравенство (4).
, будут одновременно выполняться и неравенство (3) и неравенство (4).
Неравенство (3) можно представить в виде: 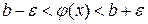 .
.
Неравенство (4) можно представить в виде: 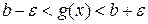 .
.
Они выполняются одновременно, причем по условию выполняется неравенство (*). Тогда для любого 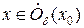 получаем:
получаем:
|
|
|
|
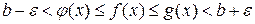 .
.  Таким образом, имеем: для любого
Таким образом, имеем: для любого  :
: 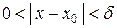 выполняется
выполняется 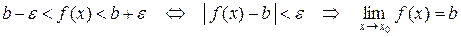 .
.
 2015-02-14
2015-02-14 1341
1341