2015-02-14
590
Определение 1. Функция 
называется б/м функцией при 
, если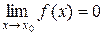 
.
Пример. Функци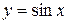и 
и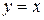 
являются б/м при 
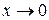, т.к. 
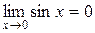и 
.
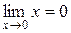Теорема 1. Пусть , 
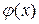– б/м функции при . Тогда:
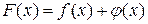– б/м функция при .
Доказательство. Рассмотрим произвольное число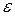 
. Тогда:
для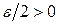 
существует 
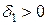такое, что для любого 
: 
;
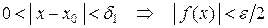для 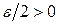существует 
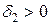такое, что для любого : 
.
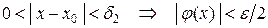Пусть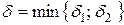 
. Тогда для любого 
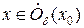имеем:
.
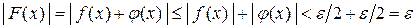Т.е. для любого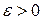 
нашли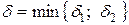 
такое, что для всех 
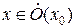выполняется неравенство 
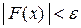. Следовательно, 
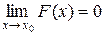, т.е. 
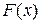– б/м функция при .
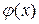Теорема 2. Пусть – б/м функция при и функция – ограничена в 
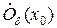, тогда 
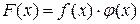– б/м функция при .
Доказательство. Пусть – б/м функция при , следовательно, .
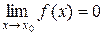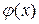– ограниченная в 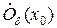функция, следовательно, существует 
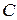: для любого 
.
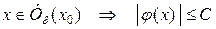Для любого 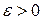рассмотрим 
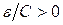. По определению предела для него существует 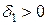такое, что для любого 
.
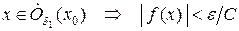Пусть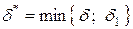 
, тогда для любого : 
.
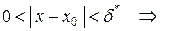
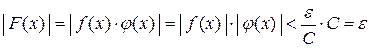Таким образом, для любого 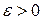существует 
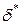такое, что для любого : 
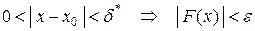. Следовательно, 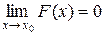, т.е. 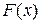– б/м функция при .
Теорема 3. Пусть – б/м функция при , функция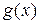 
имеет предел 
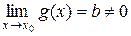. Тогда:
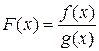– б/м функция при .
Доказательство. По условию: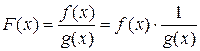 
.
Согласно теореме 2, если умножить б/м функцию на ограниченную, то получится б/м функция. Докажем, что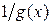 
– ограниченная в 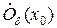функция.
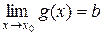, следовательно, для любого 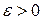существует 
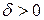такое, что для любого : 
.
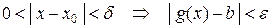Отсюда получаем:
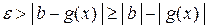, тогда 
.
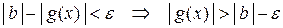Пусть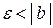 
, тогда:
, 
.
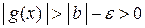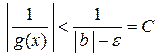Таким образом, функция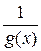 
– ограничена в 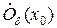, следовательно, по теореме 2, 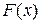– б/м функция при .
Определение 2. Функция 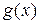называется б/б функцией при , если для любого сколь угодно большого наперед заданного числа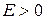 
существует 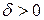такое, что для любого : 
.
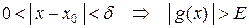Обозначение: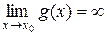 
.
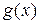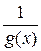Теорема 4. Пусть – б/б функция при . Тогда функция является б/м функцией при .
Доказательство. Пусть 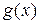– б/б функция при , т.е. для любого 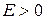, а значит и для 
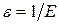существует 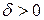такое, что для любого : 
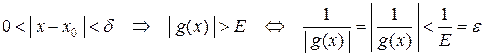, следовательно, 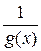является б/м функцией при .
Теорема 5. Пусть – б/м функция при . Тогда функция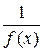 
является б/б функцией при .
Доказательство. Для любого (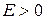
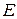– произвольное, сколь угодно большое число) существует 
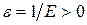. По определению б/м функции имеем: для любого 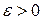существует 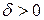такое, что для любого : 
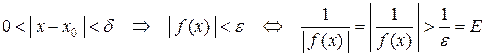. Таким образом, получили, что для любого : 
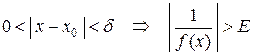, следовательно, 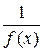является б/б функцией при .
