Теорема 1. Если функция  имеет предел в точке
имеет предел в точке  , равный
, равный 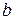 , т.е.
, т.е. 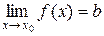 , то функцию
, то функцию  можно представить в виде
можно представить в виде 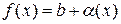 , где функция
, где функция 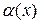 – б/м функция при
– б/м функция при  .
.
Доказательство. Пусть 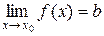 .
.
 Рассмотрим
Рассмотрим 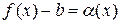 . Докажем, что
. Докажем, что 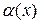 – б/м функция при
– б/м функция при  . То, что
. То, что 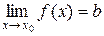 означает, что для любого
означает, что для любого 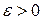 существует
существует 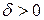 такое, что для любого
такое, что для любого  :
: 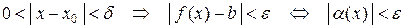 , следовательно,
, следовательно, 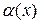 – б/м функция при
– б/м функция при  .
.
Теорема 2 (обратная к теореме 1). Если функцию  можно представить в виде суммы постоянного числа
можно представить в виде суммы постоянного числа 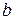 и некоторой функции
и некоторой функции 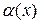 – б/м при
– б/м при  , т.е.
, т.е. 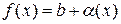 , то существует
, то существует 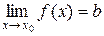 .
.
 Доказательство. Пусть функция
Доказательство. Пусть функция  представима в виде
представима в виде 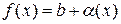 , где
, где 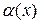 – б/м функция при
– б/м функция при  . Это значит: для любого
. Это значит: для любого 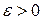 существует
существует 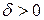 такое, что для любого
такое, что для любого  :
: 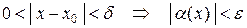
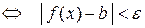 , следовательно, существует
, следовательно, существует 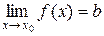 .
.
Теорема 3. Пусть 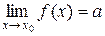 и
и 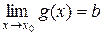 .
.
Тогда функция 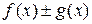 имеет в точке
имеет в точке  предел
предел
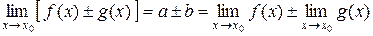 .
.
Доказательство. По теореме 1 имеем:
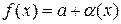 , где
, где 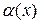 – б/м функция при
– б/м функция при  ,
,
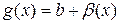 , где
, где 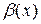 – б/м функция при
– б/м функция при  .
.
Тогда: 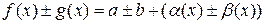 .
.
 Т.к.
Т.к. 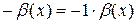
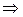 (
(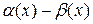 ) – б/м функция при
) – б/м функция при  ,
,

следовательно, (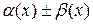 ) – б/м функция при
) – б/м функция при  . Тогда по теореме 2:
. Тогда по теореме 2:

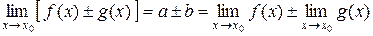 .
.
Теорема 4. Пусть 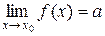 и
и 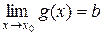 .
.
Тогда функция 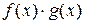 имеет в точке
имеет в точке  предел
предел
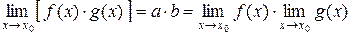 .
.
Доказательство. По теореме 1 имеем:
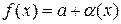 , где
, где 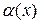 – б/м функция при
– б/м функция при  ,
,
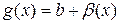 , где
, где 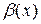 – б/м функция при
– б/м функция при  .
.
Тогда:

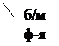
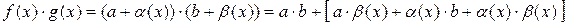 .
.
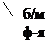 | |||||
 | |||||
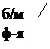 | |||||
Сумма б/м функций есть б/м функция, т.е.
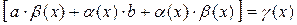 , где
, где 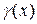 – б/м функция при
– б/м функция при  .
.
Тогда по теореме 2:

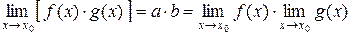 .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
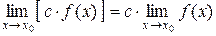 .
.
Следствие 2. Предел функции  в степени
в степени 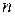 (
(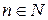 ):
):
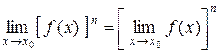 .
.
Теорема 5. Пусть 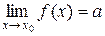 и
и 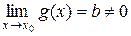 .
.
Тогда функция 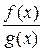 имеет предел
имеет предел
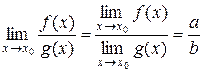 .
.
Доказательство. По теореме 1 имеем:
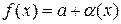 , где
, где 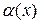 – б/м функция при
– б/м функция при  ,
,
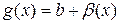 , где
, где 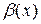 – б/м функция при
– б/м функция при  .
.
Рассмотрим:
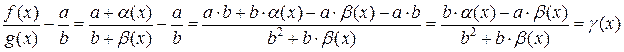

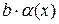 – б/м функция
– б/м функция
|

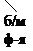
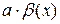 – б/м функция
– б/м функция
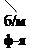

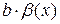 – б/м функция при
– б/м функция при  .
.
По теореме 2: 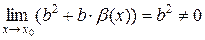 , следовательно, по теореме 3 о б/м функциях
, следовательно, по теореме 3 о б/м функциях 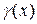 – б/м функция при
– б/м функция при  .
.
Таким образом, получили:

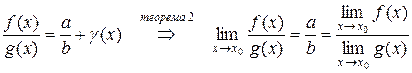 .
.
 2015-02-14
2015-02-14 718
718

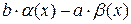 – б/м функция при
– б/м функция при 






