Пусть дана функция  , определенная в проколотой окрестности точки
, определенная в проколотой окрестности точки  .
.
Определение 1. Число 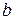 называется пределом функции
называется пределом функции  в точке
в точке  (при
(при  ), если для любого сколь угодно малого числа
), если для любого сколь угодно малого числа 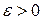 существует
существует 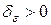 такое, что для всех
такое, что для всех  , удовлетворяющих соотношению
, удовлетворяющих соотношению 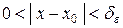 , выполняется неравенство
, выполняется неравенство 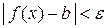 .(Рис. 12)
.(Рис. 12)
Обозначение: 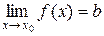 .
.
Геометрический смысл предела
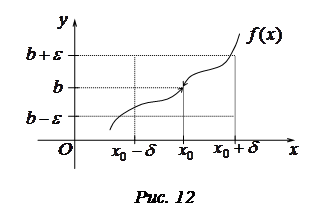
Пример 1. Доказать: 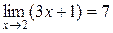 .
.
Доказательство. Для любого 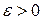 имеем:
имеем: 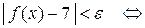
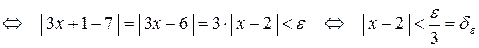 .
.
 Таким образом, для любого
Таким образом, для любого 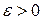 существует
существует 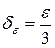 такое, что как только
такое, что как только 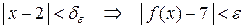 . Следовательно,
. Следовательно, 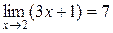 .
.
Определение 2. Число 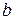 называется пределом функции
называется пределом функции  при
при 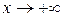 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа 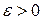 существует такое
существует такое 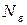 , что для всех
, что для всех 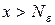 выполняется неравенство
выполняется неравенство 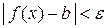 .(Рис.13)
.(Рис.13)
Геометрический смысл предела
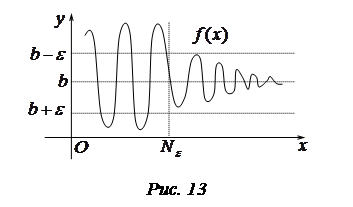
Пример 2. Доказать: 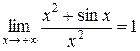 .
.
Доказательство. Для любого 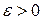 имеем:
имеем: 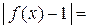
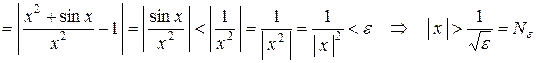 .
.
 Тогда для любого
Тогда для любого 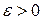 существует такое
существует такое 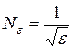 , что как только
, что как только 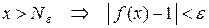 . Следовательно,
. Следовательно, 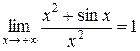 .
.
 2015-02-14
2015-02-14 1195
1195
