Теорема 2 (необходимое условие существования точки перегиба)

Если – точка перегиба функции , то либо 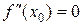, либо 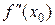не существует.

15⁰. Формула Тейлора

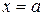Пусть функция определена в точке и некоторой ее окрестности и 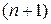раз дифференцируема в этой точке. Тогда справедливо представление:

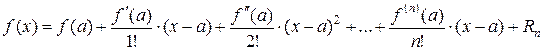, (6)

где 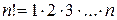, 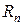– остаточный член.

Представление (6) называется формулой Тейлора.

Это разложение справедливо для любой точки из окрестности точки 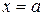. Можно доказать, что

,

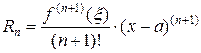где , .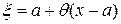

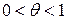Пример. Разложить функцию 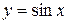по степеням .

Решение. Разложить функцию по степеням означает .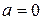

1) 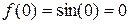; 4)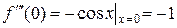

2) ; …

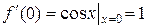3) ;

.

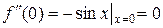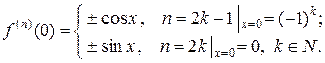
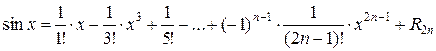15⁰. Асимптоты графика функций