Дано:
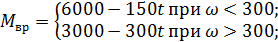
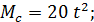
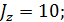
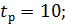
Решение:
По теореме об изменении кинетического момента в проекции на ось z, запишем
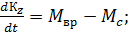 (6.1)
(6.1)
где 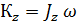 - кинетический момент тела в проекции на ось вращения.
- кинетический момент тела в проекции на ось вращения.
Для получения первой зависимости угловой скорости от времени, когда действуют два момента, умножим левую и правую части выражения (6.1) на 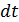 и проинтегрируем на промежутке
и проинтегрируем на промежутке 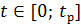 .
.
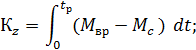
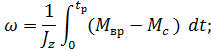
Подставляя значения моментов сил и, внеся момент инерции под знак интеграла, получим
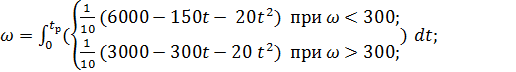 (6.2)
(6.2)
Найти значение определенного интеграла означает вычисление площади под интегральной кривой. В методе трапеций определяют шаг интегрирования и в точках деления вычисляют значения 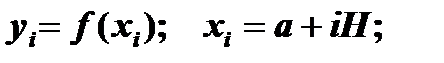 (i=0,…,N) площадь фигуры вычисляют по выражению:
(i=0,…,N) площадь фигуры вычисляют по выражению:
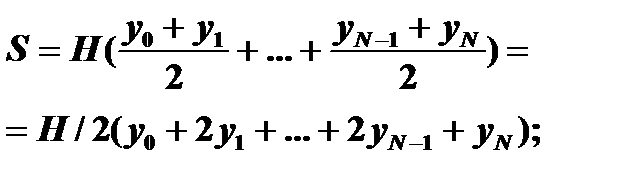
| y |
| a |
| b x |
| xi-1xi xi+1 |
Рис. 6.2. Метод трапеций
В программе вычислении интеграла (6.2) реализуется накоплением конечной суммы Iny, которое происходит в цикле с добавлением площади очередной трапеции с высотой равной шагу h1 и основаниями Y[i],Y[i-1] (ПРИЛОЖЕНИЕ 4):
for(i=1;i<n+1;i++)
{
Iny[i] = Iny[i - 1] + (Y[i] + Y[i - 1]) / 2 * h1;
}
где Y[i], Y[i - 1] – элементы массива в котом хранятся значения подынтегрального выражения. Все промежуточные значения угловой скорости на каждом шаге заносим в таблицу результаов вычисления по выражению:
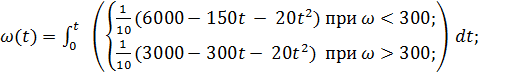 (6.3)
(6.3)
Таблица полученных значений интеграла с переменным верхним пределом служит основой для построения первого графика – разгона тела до угловой скорости 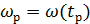 . Это конечное значение
. Это конечное значение 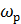 является начальным условием для второго участка движения, когда тело замедляет вращение под действием только момента
является начальным условием для второго участка движения, когда тело замедляет вращение под действием только момента 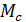 :
:
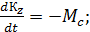 (6.4)
(6.4)
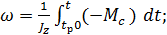
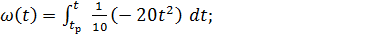 (6.5)
(6.5)
По графику и таблице находим время до остановки тела 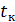 . Уточняем диапазон построения для второго графика и пересчитываем значения интеграла (6.5) на промежутке
. Уточняем диапазон построения для второго графика и пересчитываем значения интеграла (6.5) на промежутке 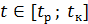 . Третий график строим для случая отсутствия сопротивления:
. Третий график строим для случая отсутствия сопротивления:
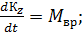 (6.6)
(6.6)
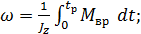
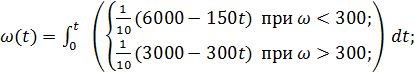 (6.7)
(6.7)
на промежутке 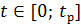 .
.
Для вычисления трех разных случаев движения используем одну процедуру вычисления интеграла, с тремя исходными функциями, которые по выбору пользователем радио-кнопки вызываются в эту процедуру как параметр-функция. Реализуя данный подход, используем класс языка C#, называемый делегатом. Выражение функции 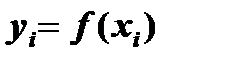 зависит в программе от выбора пользователем одного из вариантов радио-кнопки. Поэтому функция передается в процедуру вычисления интеграла с помощью делегата.
зависит в программе от выбора пользователем одного из вариантов радио-кнопки. Поэтому функция передается в процедуру вычисления интеграла с помощью делегата.
Делегат исполняет роль процедурного типа, когда процедура или функция используется как параметр в другой процедуре. При создании делегата указывается имя метода и набор параметров соответствующих типов.
Объявление делегата:
[модификаторы] delegate <тип><имя>(<параметры>);
где [модификаторы] – модификаторы доступа к делегату (как правило public),
<имя> - уникальный идентификатор,
<тип> - тип возвращаемого результата,
<параметры> - формальные параметры вызова.
Например:
public delegate Double y(Double x1, Double x2);
Описание экземпляра делегата:
y fx;
Создание экземпляра и инициализация функцией fx1(x1) с помощью умалчиваемого конструктора:
fx = new y(fx1);
Обращение к процедуре с параметром функцией fx (экземпляром делегата):
Integral(a, b, h, fx);
Причем в заголовке процедуры при ее описании используется делегат y:
void Integral(double a1, double b1, double h1, y f)
{
...
Y[i] = f(T[i],Iny[i-1]);
...
}
Функции которые передаются в процедуру Integral посредством экземпляра делегата fx имеют такую же сигнатуру, что и делегат, например для выражения (6.3):
double fx1(Double x1, Double x2)
{
if (x2 < 300)
{
return 600 - 15 * x1-2*x1*x1;
}
else
{
return 300-30*x1-2*x1*x1;
}
Делегат представляет собой разновидность класса: будучи типом он определяет сигнатуру функции. Любая функция, соответствующая этой сигнатуре может использоваться в качестве параметра конструктора класса-делегата при создании экземпляра-делегата: fx = new y(fx1);.
Элементы управления и экранная форма программы представлены на рис. 6.3.
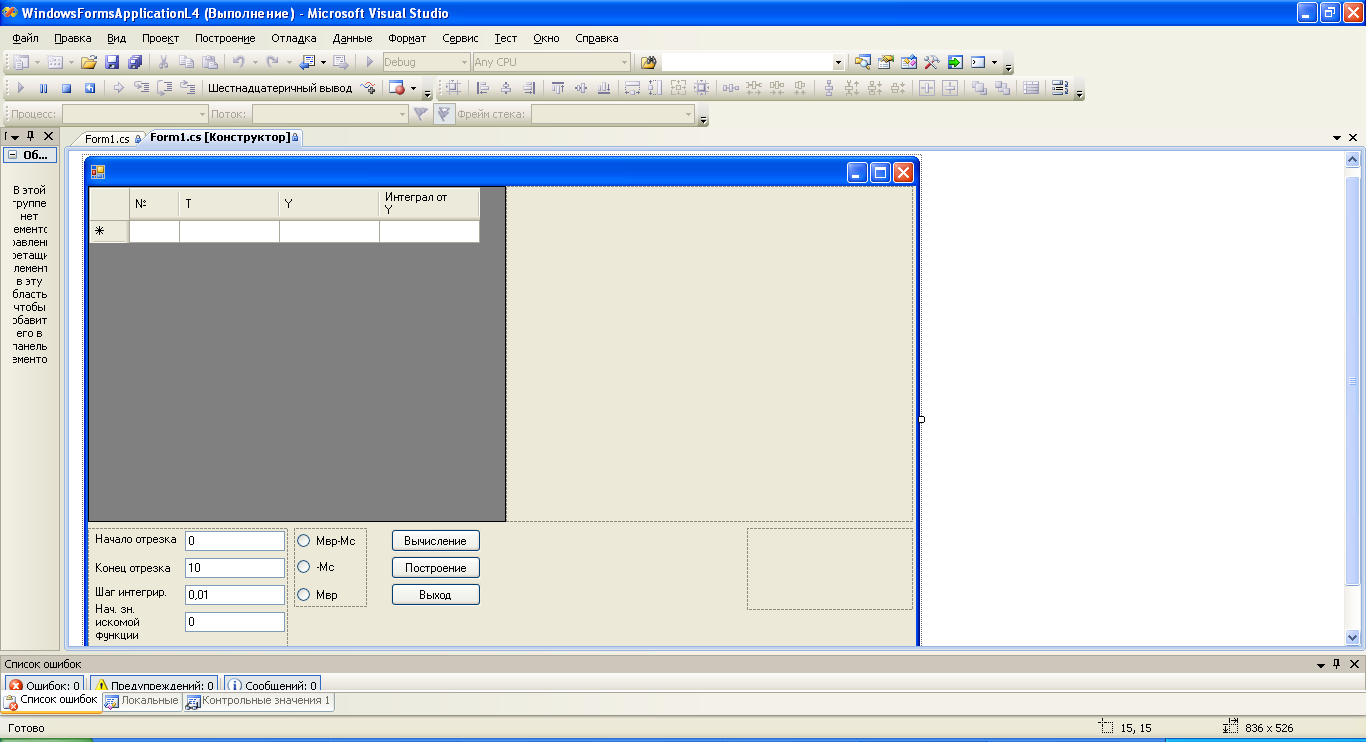
Рис. 6.3. Элементы управления в конструкторе проекта.
Текст клиентского кода программы вычисления определённого интеграла с переменным верхним пределом, которая предоставляет пользователю выбор подынтегрального выражения приведен в ПРИЛОЖЕНИИ 4.
Результаты выполнения программы представлены на Рис. 6.4, 6.5, 6.6:
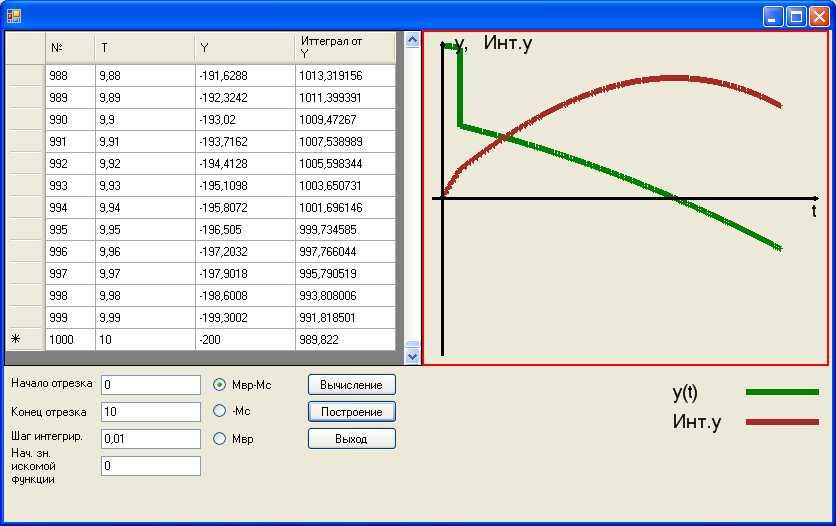
Рис. 6.4. Закон изменения угловой скорости на промежутке 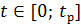 .
.
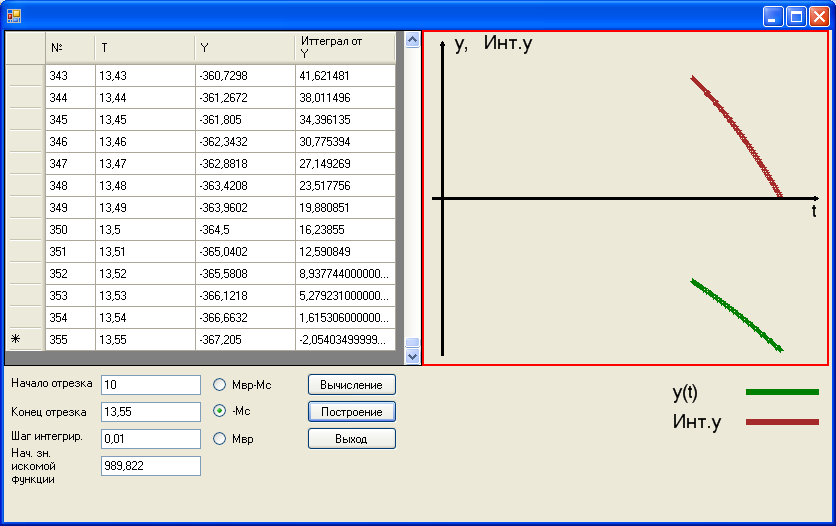 Рис. 6.5. Закон изменения угловой скорости от
Рис. 6.5. Закон изменения угловой скорости от 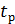 до момента остановки
до момента остановки 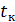 .
.
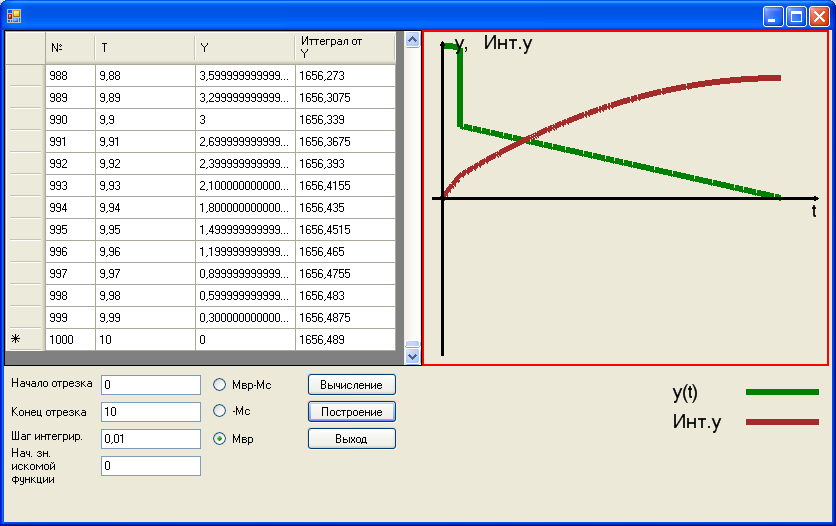
Рис. 6.6 Зависимость угловой скорости 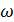 от времени от
от времени от 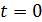 до момента
до момента 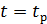 при отсутствии момента сил сопротивления
при отсутствии момента сил сопротивления 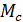 .
.
 2015-02-14
2015-02-14 278
278








