Функция 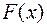 называется первообразной для функции
называется первообразной для функции  на некотором промежутке, если для всех значений
на некотором промежутке, если для всех значений 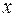 из этого промежутка выполняется равенство
из этого промежутка выполняется равенство 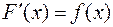 .
.
Например, функция 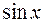 является первообразной для функции
является первообразной для функции 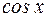 , так как при любом
, так как при любом 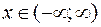
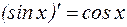 .
.
Можно заметить, что первообразной для 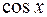 является не только
является не только 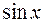 но и функция
но и функция 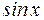 + С, где С – любая постоянная. Это справедливо для любой функции
+ С, где С – любая постоянная. Это справедливо для любой функции  , имеющей первообразную.
, имеющей первообразную.
Теорема. Пусть 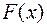 является первообразной для функции
является первообразной для функции  в некотором интервале
в некотором интервале 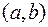 . Тогда функция
. Тогда функция 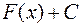 , где С – любая постоянная, также будет первообразной для
, где С – любая постоянная, также будет первообразной для  .
.
Из теоремы следует, что любые две первообразные для одной и той же функции могут отличаться друг от друга только на постоянное слагаемое.
Если 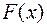 – первообразная для функции
– первообразная для функции  , то совокупность всех первообразных
, то совокупность всех первообразных 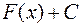 , где С – произвольная постоянная, называется неопределенным интегралом от функции
, где С – произвольная постоянная, называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 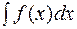 . Таким образом,
. Таким образом, 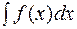 =
= 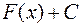 .
.
Функция  называется подынтегральной функцией, произведение
называется подынтегральной функцией, произведение 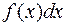 – подынтегральным выражением, переменная
– подынтегральным выражением, переменная 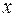 – переменной интегрирования, а символ
– переменной интегрирования, а символ 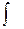 – знаком интеграла.
– знаком интеграла.
Операция нахождения неопределенного интеграла от данной функции называется интегрированием функции  .Операция интегрирования является обратной к операции дифференцирования.
.Операция интегрирования является обратной к операции дифференцирования.
Свойства неопределенного интеграла:
1. 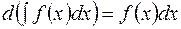
2. 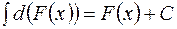
3. 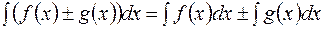
4. 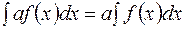 ,
, 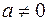 ,
, 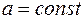
5. Если 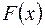 первообразная для
первообразная для 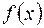 , тогда
, тогда
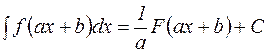 ,
, 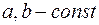
Таблица основных неопределенных интегралов:
1. 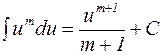 ;
; 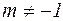
2. 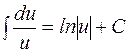
3. 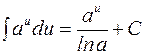
4. 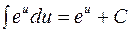
5. 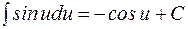
6. 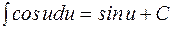
7. 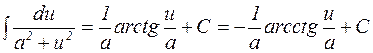 ,
, 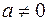
8. 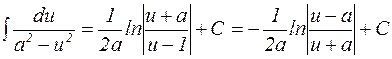
9. 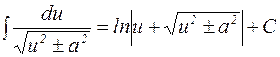 ,
, 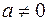
10. 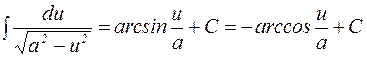 ,
, 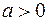
11. 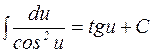
12. 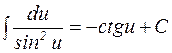
13. 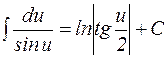
14. 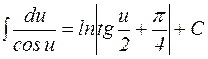
Здесь и – функция от х, но на ее месте может быть и независимая переменная х.
Интегралы от некоторых элементарных функций не являются элементарными функциями, например:
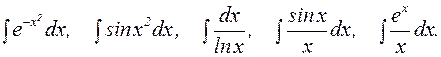
Такие интегралы еще называются неберущимися.
Рассмотрим основные методы интегрирования.
 2015-02-04
2015-02-04 352
352








