Рассмотрим функцию двух переменных 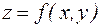 , определенную в некоторой области
, определенную в некоторой области 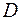 , являющейся частью плоскости XOY. Частной производной от функции
, являющейся частью плоскости XOY. Частной производной от функции 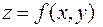 по независимой переменной х называется производная
по независимой переменной х называется производная
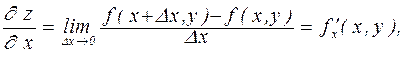
вычисленная при постоянном у.
Частной производной по у называется производная
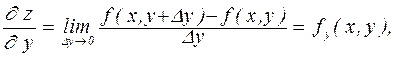
вычисленная при постоянном х.
Для частных производных справедливы обычные правила и формулы дифференцирования.
При изменении 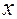 и
и 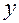 частные производные сами являются функциями, и можно вычислять частные производные от этих функций. Частные производные второго порядка обозначают следующим образом:
частные производные сами являются функциями, и можно вычислять частные производные от этих функций. Частные производные второго порядка обозначают следующим образом:
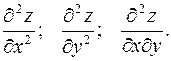
Последнюю из трех частных производных второго порядка называют смешанной производной. Если частные производные второго порядка непрерывны в точке 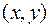 , тогда
, тогда 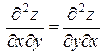 , то есть не важно, в какой последовательности вычисляется смешанная производная.
, то есть не важно, в какой последовательности вычисляется смешанная производная.
Градиентом функции 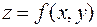 в точке
в точке 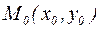 называется вектор, координатами которого являются частные производные:
называется вектор, координатами которого являются частные производные:
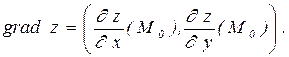
Этот вектор указывает в точке М0 направление наискорейшего роста функции 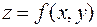 .
.
Для функции двух переменных вводится понятие производной по направлению, аналогичное понятию частной производной, когда приращение аргумента задается вдоль данного направления. Для любого направления, задаваемого вектором 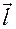 , производная функции
, производная функции 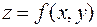 в точке
в точке 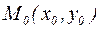 по направлению этого вектора может быть выражена следующим образом:
по направлению этого вектора может быть выражена следующим образом:
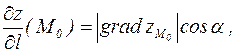
где знак модуля означает длину вектора градиента в точке 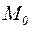 , а
, а 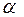 – угол между градиентом и направлением
– угол между градиентом и направлением 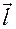 .
.
Пример. Найти градиент функции 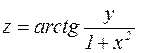 в точке
в точке 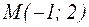 .
.
Решение: Рассматривая у как постоянную величину, дифференцируем функцию по переменной х.
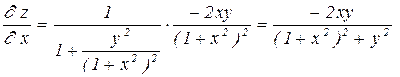 .
.
Аналогично, рассматривая х как постоянную величину, получаем:
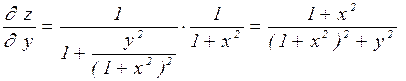 .
.
Находим значения частных производных в точке 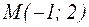 :
:
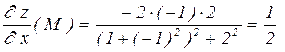 ,
,
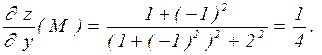
Ответ: 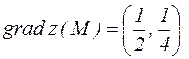 .
.
 2015-02-04
2015-02-04 359
359








