4.1 – 4.20. Найти следующие пределы.
4.1 а) 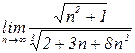 б)
б) 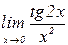
4.2. а) 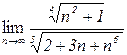 б)
б) 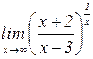
4.3. а) 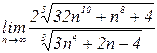 б)
б) 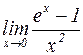
4.4. а) 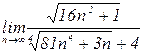 б)
б) 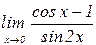
4.5. а) 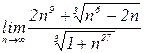 б)
б) 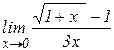
4.6. а) 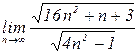 б)
б) 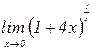
4.7. а) 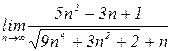 б)
б) 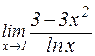
4.8. а) 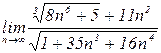 б)
б) 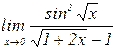
4.9. а) 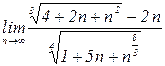 б)
б) 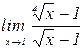
4.10. а) 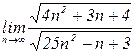 б)
б) 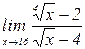
4.11. а) 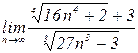 б)
б) 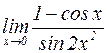
4.12. а) 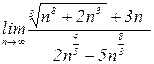 б)
б) 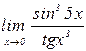
4.13. а) 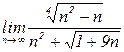 б)
б) 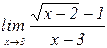
4.14. а) 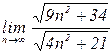 б)
б) 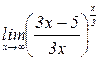
4.15. а) 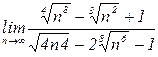 б)
б) 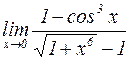
4.16. а) 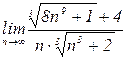 б)
б) 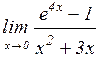
4.17. а) 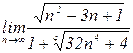 б)
б) 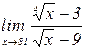
4.18. а) 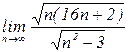 б)
б) 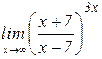
4.19. а) 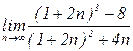 б)
б) 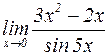
4.20. а) 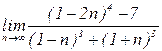 б)
б) 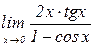
Указания к задаче 4: предел функции, предел последовательности.
Областью определения функции 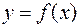 называют те значения
называют те значения 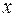 , для которых данное выражение имеет смысл и значения
, для которых данное выражение имеет смысл и значения 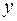 конечны. Пусть функция
конечны. Пусть функция 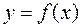 определена в некоторой окрестности точки
определена в некоторой окрестности точки 
 . Если для любого числа
. Если для любого числа 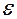 > 0 найдется такое число
> 0 найдется такое число 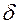 > 0, что при всех
> 0, что при всех 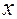 , удовлетворяющих неравенству
, удовлетворяющих неравенству 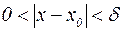 , будет выполнено неравенство
, будет выполнено неравенство 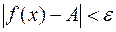 , то число
, то число 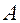 называют пределом функции
называют пределом функции  в точке
в точке  , то есть
, то есть
A = 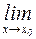
 .
.
Число В называется левосторонним пределом функции  в точке
в точке  , если для любого числа
, если для любого числа 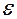 > 0 найдется такое число
> 0 найдется такое число 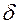 > 0, что при всех
> 0, что при всех 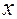 , удовлетворяющих неравенству
, удовлетворяющих неравенству 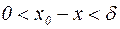 , будет выполнено неравенство
, будет выполнено неравенство 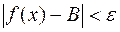 . Левосторонний предел обозначают следующим образом:
. Левосторонний предел обозначают следующим образом: 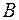 =
= 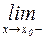
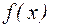 .
.
Аналогично, число 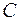 называется правосторонним пределом функции
называется правосторонним пределом функции  в точке
в точке  , если для любого числа
, если для любого числа 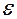 > 0 существует числосла
> 0 существует числосла 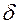 > 0, такое, что из неравенства
> 0, такое, что из неравенства 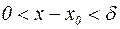 следует
следует 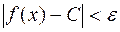 и С =
и С = 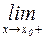
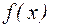 .
.
Например, для функции 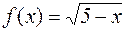 в точке
в точке 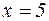 имеет смысл говорить только о левостороннем пределе, а для функции
имеет смысл говорить только о левостороннем пределе, а для функции 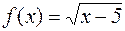 в точке
в точке 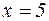 – только о правостороннем.
– только о правостороннем.
Можно доказать, что для существования предела функции  в точке
в точке 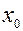 необходимо и достаточно, чтобы существовали и были равны левосторонний и правосторонний пределы в этой точке.
необходимо и достаточно, чтобы существовали и были равны левосторонний и правосторонний пределы в этой точке.
Если для любого числа 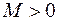 существует число
существует число 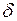 > 0, такое, что при всех значениях
> 0, такое, что при всех значениях 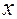 из
из 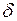 -окрестности
-окрестности 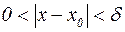 будет выполнено условие
будет выполнено условие 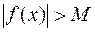 , то предел функции
, то предел функции  в точке
в точке  равен бесконечности:
равен бесконечности: 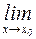
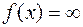 .
.
Если же для любого числа 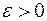 существует число
существует число 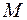 , такое, что при всех
, такое, что при всех 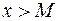
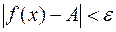 , то
, то 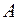 является пределом функции
является пределом функции  при
при 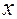 , стремящемся к бесконечности:
, стремящемся к бесконечности: 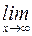
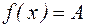 .
.
Важным частным случаем последнего определения является предел числовой последовательности. Если функция  задана на множестве натуральных чисел, то такую функцию называют числовой последовательностью
задана на множестве натуральных чисел, то такую функцию называют числовой последовательностью 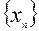 (
(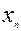 =
= 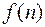 )
)  , а ее предел
, а ее предел 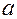 – пределом последовательности
– пределом последовательности 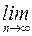
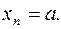 Таким образом, число
Таким образом, число 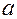 является пределом последовательности, если для любого числа
является пределом последовательности, если для любого числа 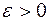 существует число
существует число 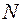 , такое, что при всех
, такое, что при всех 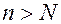 выполняется неравенство
выполняется неравенство 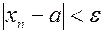 .
.
Отметим следующие свойства пределов (эти свойства справедливы в том случае, если существуют пределы указанных функций):
1. Если 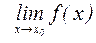 существует, то он единственный.
существует, то он единственный.
2. 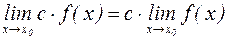 (
(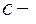 постоянное число);
постоянное число);
3. 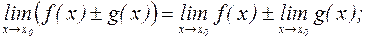
4. 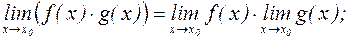
5. 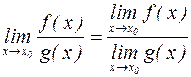 (
(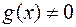 ).
).
Дадим несколько определений, важных для дальнейшего.
Функция  называется бесконечно малой в окрестности точки
называется бесконечно малой в окрестности точки  , если
, если 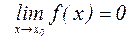 .
.
Функция  называется бесконечно большой в окрестности точки
называется бесконечно большой в окрестности точки  , если
, если 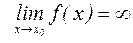 .
.
Функция  называется ограниченной в окрестности точки
называется ограниченной в окрестности точки  , если существует число
, если существует число 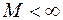 , такое, что
, такое, что 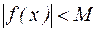 при всех
при всех 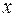 из этой окрестности.
из этой окрестности.
Для вычисления пределов важны следующие свойства бесконечно малых величин. Пусть 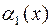 и
и 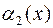 – бесконечно малые, а
– бесконечно малые, а  – ограниченная функция в окрестности точки
– ограниченная функция в окрестности точки  . Тогда верны утверждения:
. Тогда верны утверждения:
1. 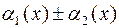 – бесконечно малая величина в окрестности точки
– бесконечно малая величина в окрестности точки  ;
;
2. 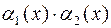 – бесконечно малая величина в окрестности точки
– бесконечно малая величина в окрестности точки  ;
;
3. 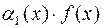 ─ бесконечно малая величина в окрестности точки
─ бесконечно малая величина в окрестности точки  ;
;
4. Если существует 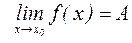 , то это равносильно тому, что в окрестности точки
, то это равносильно тому, что в окрестности точки 
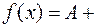
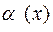 , где
, где 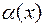 – бесконечно малая величина в окрестности этой точки;
– бесконечно малая величина в окрестности этой точки;
5. Для монотонно возрастающей функции (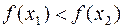 при
при 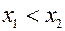 ) или монотонно убывающей (
) или монотонно убывающей (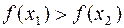 при
при 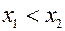 ) в окрестности точки
) в окрестности точки  всегда существует
всегда существует 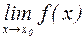 , который конечен, если
, который конечен, если  ограничена в окрестности точки
ограничена в окрестности точки  .
.
Рассмотрим две бесконечно малые величины 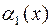 и
и 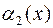 в окрестности точки
в окрестности точки  . Если
. Если 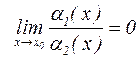 , то говорят, что
, то говорят, что 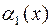 – величина более высокого порядка малости, чем
– величина более высокого порядка малости, чем 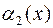 . Записывают это следующим образом:
. Записывают это следующим образом:
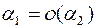 .
.
Если 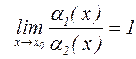 , то
, то 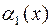 и
и 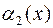 называют эквивалентными бесконечно малыми величинами в окрестности точки
называют эквивалентными бесконечно малыми величинами в окрестности точки  , то есть
, то есть
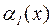 ~
~ 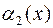 при
при 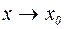 .
.
Также следует знать, что величина, обратная бесконечно малой является бесконечно большой, а величина, обратная бесконечно большой является бесконечно малой величиной.
Рассмотрим несколько примеров.
Пример 1. Вычислить предел 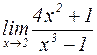 .
.
Решение: Очевидно, что числитель дроби 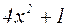 при
при 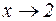 стремится к
стремится к 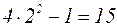 . Аналогично знаменатель стремится к
. Аналогично знаменатель стремится к 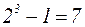 . Тогда вся дробь будет стремиться к
. Тогда вся дробь будет стремиться к 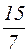 . Таким образом,
. Таким образом, 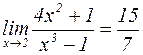 .
.
Здесь мы использовали свойства пределов, о которых говорилось выше.
Пример 2. Вычислить предел 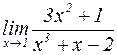 .
.
Решение: Очевидно, 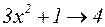 , а
, а 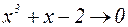 при
при 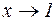 . Таким образом, дробь будет стремиться к бесконечности, так как знаменатель – бесконечно малая величина, а обратная ей величина – бесконечно большая.
. Таким образом, дробь будет стремиться к бесконечности, так как знаменатель – бесконечно малая величина, а обратная ей величина – бесконечно большая.
Поскольку числитель в окрестности точки 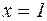 ограничен, получаем:
ограничен, получаем: 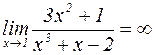 .
.
Пример 3: Вычислить предел 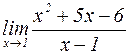 .
.
Решение: Если подставить 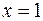 в рассматриваемую функцию, то получим нуль в числителе и в знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностью вида
в рассматриваемую функцию, то получим нуль в числителе и в знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностью вида 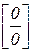 . Встречаются также неопределенности вида
. Встречаются также неопределенности вида 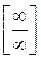 ,
, 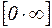 ,
, 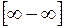 ,
, 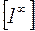 и другие, для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенности.
и другие, для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенности.
Вернемся к примеру. Разложим числитель на множители:
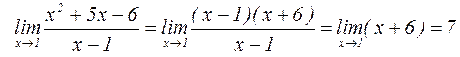 .
.
Рассмотрим 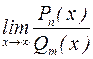 , где
, где 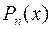 и
и 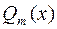 – многочлены степени
– многочлены степени 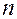 и
и 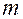 :
: 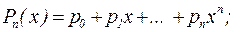
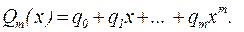
Пусть 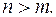 Разделим числитель и знаменатель почленно на
Разделим числитель и знаменатель почленно на 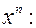
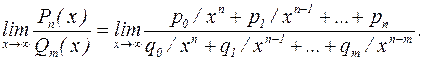
Нетрудно видеть, что при 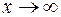 все слагаемые числителя, кроме последнего, стремятся к нулю, а в знаменателе все слагаемые стремятся к нулю. Таким образом,
все слагаемые числителя, кроме последнего, стремятся к нулю, а в знаменателе все слагаемые стремятся к нулю. Таким образом, 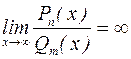 по аналогии с примером 2.
по аналогии с примером 2.
Если 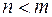 , то
, то 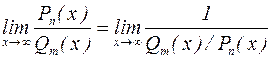 , а дробь в знаменателе имеет уже степень числителя большую, чем степень знаменателя и, согласно только что рассмотренному случаю, стремится к бесконечности. Тогда имеем:
, а дробь в знаменателе имеет уже степень числителя большую, чем степень знаменателя и, согласно только что рассмотренному случаю, стремится к бесконечности. Тогда имеем:
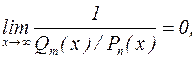 так как величина, обратная бесконечно большой, есть бесконечно малая величина.
так как величина, обратная бесконечно большой, есть бесконечно малая величина.
Рассмотрим теперь случай 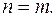 Поделив числитель и знаменатель почленно на
Поделив числитель и знаменатель почленно на 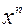 , получим:
, получим:
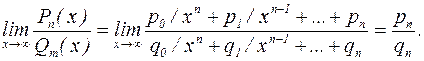
Таким образом, 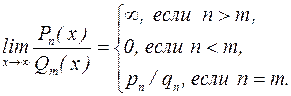
Рассмотрим два предела: 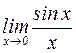 и
и 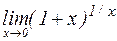 .
.
С помощью несложных оценок можно показать, что 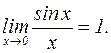 Вычисление второго предела требует бóльших усилий, но можно доказать, что он равен числу
Вычисление второго предела требует бóльших усилий, но можно доказать, что он равен числу 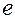 (основанию натурального логарифма):
(основанию натурального логарифма): 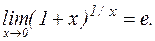 Доказательства можно найти в учебниках по математическому анализу.
Доказательства можно найти в учебниках по математическому анализу.
В силу важности этих пределов их называют замечательными пределами. Используя замечательные пределы, можно получить следующие результаты:
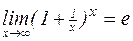 ;
; 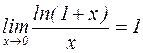 ;
; 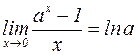 ;
;
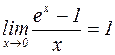 ;
; 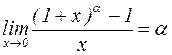 .
.
Используя эти и другие соотношения можно получить таблицу эквивалентных функций при 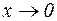 :
:
1. 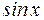 ~
~ 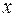 ,
,
2. tg 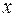 ~
~ 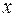 ,
,
3. arcsin 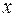 ~
~ 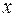 ,
,
4. arctg 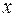 ~
~ 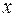 ,
,
5 .1-cosx ~ x2/2,
6. 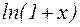 ~
~ 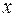 ,
,
7. 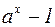 ~
~ 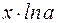 ,
,
8. 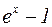 ~
~ 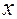 ,
,
9. 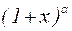 ~
~ 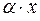 .
.
Бесконечно большой многочлен (при 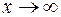 ) эквивалентен своей старшей степени с коэффициентом.
) эквивалентен своей старшей степени с коэффициентом.
Например, при 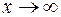 3х5+2х2–8 ~ 3х5.
3х5+2х2–8 ~ 3х5.
При вычислении пределов можно использовать эти соотношения эквивалентности, заменяя, например, отношения бесконечно малых (бесконечно больших) на отношения эквивалентных им бесконечно малых (бесконечно больших) величин.
Пример 4. Вычислить предел:
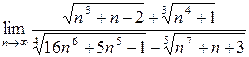 .
.
Решение: 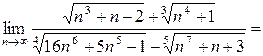
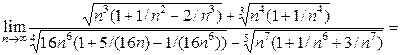
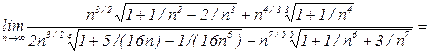
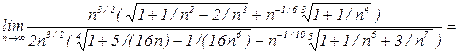
Очевидно, что все подкоренные выражения при 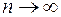 стремятся к единице, а вторые слагаемые в скобках – к нулю. Поэтому последний предел равен следующему:
стремятся к единице, а вторые слагаемые в скобках – к нулю. Поэтому последний предел равен следующему:
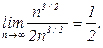
Этот предел можно вычислить другим способом – все многочлены в подкоренных выражениях заменить старшими степенями с коэффициентами (используем эквивалентные функции), затем числитель и знаменатель также заменить старшими степенями с коэффициентами. Выглядит это так:
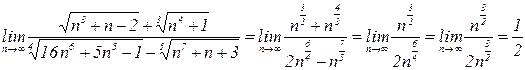
Пример 5. Вычислить предел 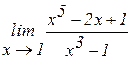 .
.
Решение: Подставив в заданную функцию 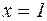 , убеждаемся, что имеем дело с неопределенностью вида
, убеждаемся, что имеем дело с неопределенностью вида 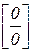 . Известно, что если
. Известно, что если
 – корень многочлена
– корень многочлена 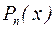 , то
, то 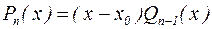 , где
, где 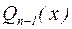 – многочлен степени
– многочлен степени 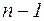 .
.
Следовательно, 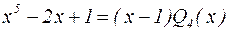 . Проще всего узнать вид многочлена
. Проще всего узнать вид многочлена 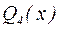 , разделив
, разделив 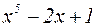 на
на 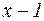 . Это можно сделать, выполнив деление «столбиком», как делят числа:
. Это можно сделать, выполнив деление «столбиком», как делят числа:

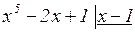
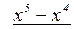
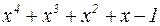

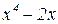
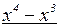
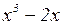
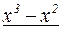
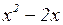
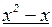
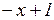
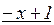
0
Следовательно, 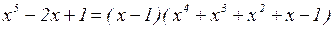 . Тогда, раскладывая на множители разность кубов в знаменателе, получим:
. Тогда, раскладывая на множители разность кубов в знаменателе, получим:
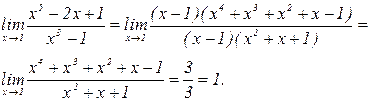
Пример 6. Вычислить предел
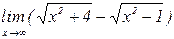 .
.
Решение: Это неопределенность вида 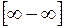 . Домножим и поделим функцию, стоящую под знаком предела, на сопряженную сумму
. Домножим и поделим функцию, стоящую под знаком предела, на сопряженную сумму 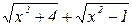 :
:
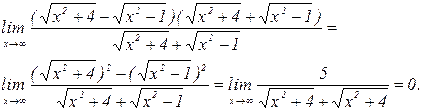
В последнем равенстве мы получили деление 5 на бесконечность. Это можно рассмотреть, как умножение 5 на величину, обратную бесконечно большой – т.е. на 0 (бесконечно малую), поэтому получили 0.
Пример 7. Вычислить предел
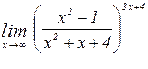 .
.
Решение: В данном случае имеем дело с неопределенностью вида 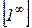 . Преобразуем выражение в скобках, выделив единицу и бесконечно малую функцию:
. Преобразуем выражение в скобках, выделив единицу и бесконечно малую функцию:
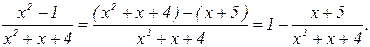
Тогда
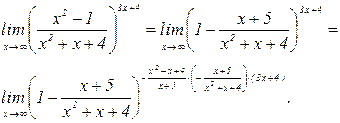
Так как при 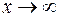
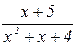 – бесконечно малая величина (степень знаменателя больше степени числителя), то
– бесконечно малая величина (степень знаменателя больше степени числителя), то
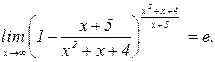
Поскольку 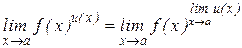 , получаем:
, получаем:
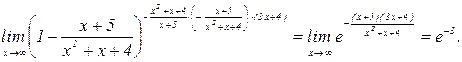
Пример 8. Найти предел
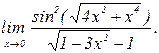
Решение: Неопределенность вида 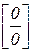 . При
. При 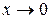
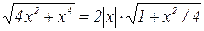 ~
~ 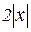 . Поэтому
. Поэтому 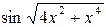 ~
~ 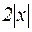 .
.
Далее, 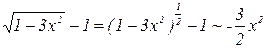 .
.
Поэтому
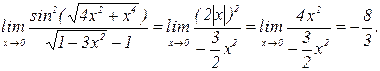
 2015-02-04
2015-02-04 834
834








