Однородным уравнением первого порядка называется уравнение вида:
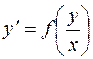 . (6)
. (6)
Для его решения введем новую переменную 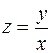 . Тогда
. Тогда 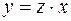 и
и 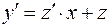 . Подставляя эти соотношения в (6), получаем:
. Подставляя эти соотношения в (6), получаем: 
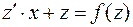 или
или 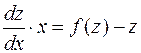 . Это уравнение с разделяющимися переменными, и оно легко интегрируется. Найдя
. Это уравнение с разделяющимися переменными, и оно легко интегрируется. Найдя 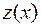 , получаем искомое решение
, получаем искомое решение 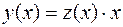 .
.
Пример 2. Решить уравнение: 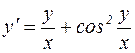 .
.
Решение: Полагая 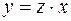 и
и 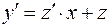 , получим:
, получим:
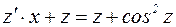 , или
, или 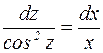 .
.
Интегрируя обе части последнего уравнения, получим:
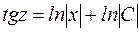 .
.
Для удобства, произвольная постоянная здесь представлена в виде 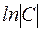 , где
, где 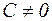 . Тогда
. Тогда 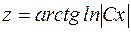 и окончательно общее решение принимает вид:
и окончательно общее решение принимает вид:
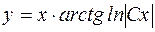 .
.
Пример 3. Решить уравнение: 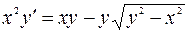 .
.
Решение: Пусть 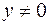 . Разделим обе части уравнения на
. Разделим обе части уравнения на 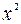 :
:
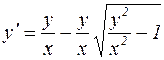 .
.
После замены переменной 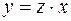 это уравнение приводится к виду:
это уравнение приводится к виду:
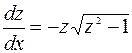 , или
, или 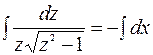 .
.
Вычислим интеграл в левой части последнего уравнения:

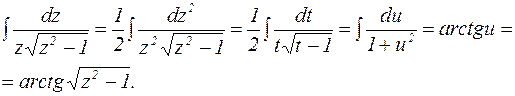
Тогда 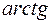
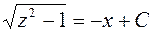 .
.
Заметим, что общее решение уравнения можно записать в виде функции, заданной неявно (подставим 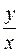 вместо z):
вместо z):
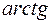
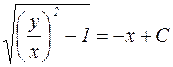 .
.
 2015-02-04
2015-02-04 338
338








