Уравнение с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:

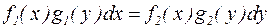
Для его решения следует сначала разделить переменные, то есть разнести их в разные стороны уравнения:

( ),

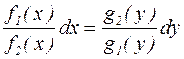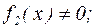
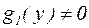а затем проинтегрировать обе части уравнения:

.

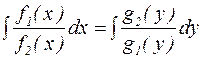Следует иметь в виду, что полученные неопределенные интегралы могут различаться на произвольную постоянную .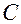

Пример 1. Решить задачу Коши: , .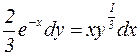

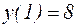Решение: Поделим обе части уравнения на 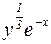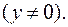Тогда:

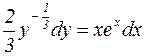и .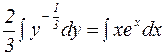

Вычисляя интегралы, находим: 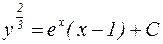. Отсюда получаем общее решение:

.

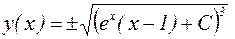Так как, по условию, 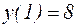>0, то выбираем знак «+»:

.

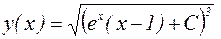Подставим в это решение начальное условие:

;

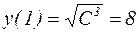Следовательно, 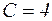и 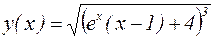– искомое частное решение, то есть решение задачи Коши.