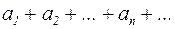 (2)
(2)
Называется бесконечным числовым рядом, а сами числа (1) – членами ряда.
Вместо (2), пользуясь знаком суммы, часто пишут так:
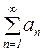 ,
,
при этом формулу 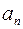 , позволяющую получить любой член ряда при подстановке в нее соответствующего фиксированного значения n, называется общим членом ряда.
, позволяющую получить любой член ряда при подстановке в нее соответствующего фиксированного значения n, называется общим членом ряда.
Сумма конечного числа первых n членов называется n - ой частичной суммой ряда:
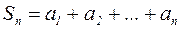
Если существует конечный предел последовательности частичных сумм ряда 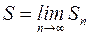 , то его называют суммой ряда и ряд называется сходящимся. Если этот предел не существует или равен бесконечности, то говорят, что ряд расходится.
, то его называют суммой ряда и ряд называется сходящимся. Если этот предел не существует или равен бесконечности, то говорят, что ряд расходится.
Заметим, что здесь, говоря о 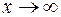 , имеем ввиду, что
, имеем ввиду, что 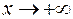 .
.
Рассмотрим основные свойства сходящихся рядов:
1. На сходимости ряда не сказывается отбрасывание конечного числа его членов.
2. Сходимость ряда не нарушится, если все его члены умножить на одно и то же ненулевое число.
3. Сумма (разность) сходящихся рядов есть ряд сходящийся.
Для установлениясходимости или расходимости рядапользуются теоремами, называемыми признаками сходимости. Рассмотрим основные из них.
1. Необходимый признак сходимости ряда.
Если ряд сходится, то предел его общего члена равен нулю при неограниченном возрастании n, т.е.
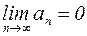 . (3)
. (3)
Условие (3) является необходимым, но не достаточным условием сходимости, поэтому если 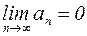 , то ряд может как сходиться, так и расходиться.
, то ряд может как сходиться, так и расходиться.
Однако, если 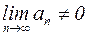 , то ряд расходится. Таким образом, пользуясь необходимым признаком сходимости, можно установить лишь расходимость данного числового ряда.
, то ряд расходится. Таким образом, пользуясь необходимым признаком сходимости, можно установить лишь расходимость данного числового ряда.
Заметим, что необходимый признак сходимости можно применять к рядам, члены которых имеют любые знаки.
Пример 1. Исследовать сходимость ряда 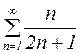 .
.
Решение: Рассмотрим предел общего члена ряда:
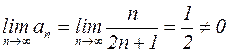 .
.
Делаем вывод, что ряд расходится.
Пример 2. Исследовать сходимость ряда 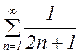 .
.
Решение: Рассмотрим предел общего члена ряда:
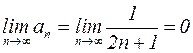 .
.
Необходимый признак не дает ответа на вопрос о сходимости данного ряда.
Сформулируем достаточные признаки сходимости некоторых рядов и вернемся к решению примера.
В первую очередь рассмотрим ряды, члены которых неотрицательны. Для краткости такие ряды мы будем называть просто положительными.
Признак сравнения 1. Рассмотрим два ряда с положительными членами 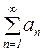 и
и 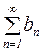 . Пусть, начиная с некоторого n, выполняется условие
. Пусть, начиная с некоторого n, выполняется условие 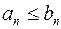 . Если ряд
. Если ряд 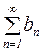 сходится, то ряд
сходится, то ряд 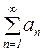 тоже сходится. Если ряд
тоже сходится. Если ряд 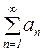 расходится, то ряд
расходится, то ряд 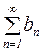 тоже расходится.
тоже расходится.
Признак сравнения 2. Если существует конечный и отличный от нуля предел 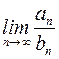 , то ряды
, то ряды 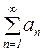 и
и 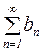 ведут себя одинаково, т.е. оба сходятся или оба расходятся.
ведут себя одинаково, т.е. оба сходятся или оба расходятся.
В частности, если 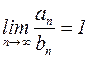 , то, как известно, при
, то, как известно, при 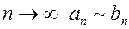 .
.
При использовании этих двух признаков нужно сравнивать исследуемый ряд с рядом, сходимость или расходимость которого уже известна.
Для сравнения обычно выбирают один из следующих рядов:
I. 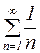 – гармонический ряд, он расходится.
– гармонический ряд, он расходится.
II. 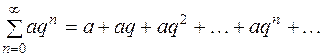 (
(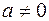 ) — геометрическая прогрессия, при
) — геометрическая прогрессия, при 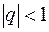 ряд сходится, при
ряд сходится, при 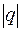
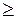 1 расходится.
1 расходится.
III. 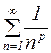 – обобщенный гармонический ряд, при
– обобщенный гармонический ряд, при 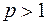 сходится, при
сходится, при 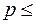 1 расходится.
1 расходится.
Пример 3. Вернемся к ряду из примера 2: 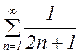 .
.
Решение: Это ряд с положительными членами. Выпишем общий член ряда и заменим его на эквивалентную величину при 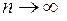 (бесконечно большой многочлен эквивалентен своей старшей степени с коэффициентом):
(бесконечно большой многочлен эквивалентен своей старшей степени с коэффициентом):
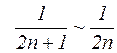
Ряд 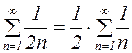 – гармонический ряд и, как известно, расходится (постоянный множитель
– гармонический ряд и, как известно, расходится (постоянный множитель 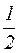 не влияет на сходимость или расходимость ряда). Следовательно, на основании второго признака сходимости исходный ряд также расходится.
не влияет на сходимость или расходимость ряда). Следовательно, на основании второго признака сходимости исходный ряд также расходится.
Пример 4. Исследовать сходимость ряда 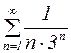 .
.
Решение: В качестве сравнения возьмем геометрическую прогрессию 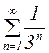 , которая сходится, т.к.
, которая сходится, т.к. 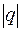 =
= 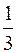
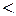 1. Сравним общие члены этих двух рядов:
1. Сравним общие члены этих двух рядов: 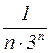
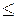
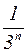 . На основании первого признака сравнения исходный ряд сходится.
. На основании первого признака сравнения исходный ряд сходится.
Пример 5. Исследовать сходимость ряда 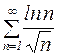 .
.
Решение: Рассмотрим расходящийся ряд 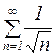 (обобщенный гармонический ряд с р = 1/2). Поскольку, начиная с n = 3, выполняется условие
(обобщенный гармонический ряд с р = 1/2). Поскольку, начиная с n = 3, выполняется условие 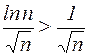 , то, согласно первому признаку сравнения, исходный ряд расходится.
, то, согласно первому признаку сравнения, исходный ряд расходится.
Признак Даламбера. Рассмотрим ряд с положительными членами 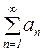 . Если существует предел
. Если существует предел 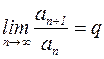 , то при q
, то при q 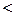 1 ряд сходится, при q
1 ряд сходится, при q 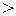 1 расходится, при q = 1 вопрос о сходимости ряда остается открытым и следует использовать другие признаки.
1 расходится, при q = 1 вопрос о сходимости ряда остается открытым и следует использовать другие признаки.
Пример 6. Исследовать сходимость ряда 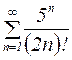 .
.
Решение: Поскольку 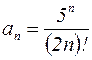 , то
, то 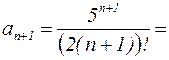
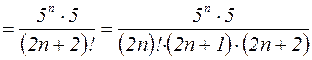 .
.
Напомним, что 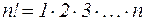 . Теперь найдем предел отношения
. Теперь найдем предел отношения 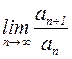 :
: 
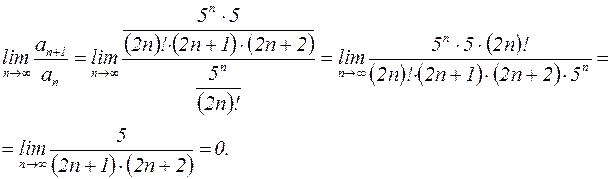
Так как 0 < 1, то, по признаку Даламбера, исходный ряд сходится.
Радикальный признак Коши. Рассмотрим ряд с положительными членами 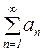 . Если существует предел
. Если существует предел 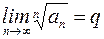 , то при q
, то при q 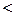 1 ряд сходится, при q
1 ряд сходится, при q 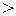 1 расходится, при q = 1 вопрос о сходимости ряда остается открытым и следует использовать другие признаки.
1 расходится, при q = 1 вопрос о сходимости ряда остается открытым и следует использовать другие признаки.
Пример 7. Исследовать сходимость ряда 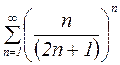 .
.
Решение: Поскольку общий член ряда содержит n -ую степень, то можно применить радикальный признак Коши.
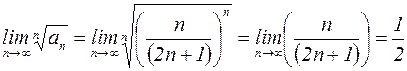
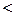 1,
1,
следовательно, ряд сходится.
Интегральный признак Коши.
Если 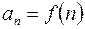 , где функция
, где функция  положительна, монотонно убывает и непрерывна при
положительна, монотонно убывает и непрерывна при 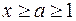 , то ряд
, то ряд 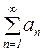 и интеграл
и интеграл 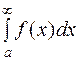 ведут себя одинаково (оба сходятся или оба расходятся).
ведут себя одинаково (оба сходятся или оба расходятся).
Заметим, что несобственный интеграл 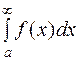 сходится, если его значение является конечным, и расходится, если его значение не существует или равно бесконечности.
сходится, если его значение является конечным, и расходится, если его значение не существует или равно бесконечности.

Пример 8. Исследовать сходимость ряда 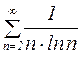 .
.
Решение: Рассмотрим функцию 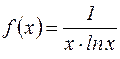 . При
. При 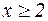 функция
функция  положительна, монотонно убывает и непрерывна, т.е. удовлетворяет условию интегрального признака Коши. Рассмотрим интеграл:
положительна, монотонно убывает и непрерывна, т.е. удовлетворяет условию интегрального признака Коши. Рассмотрим интеграл:
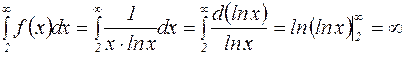 .
.
Заметим, что для вычисления выражения 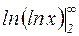 переходят к пределу:
переходят к пределу:
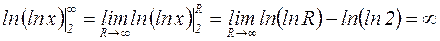 .
.
Итак, интеграл расходится. Из расходимости интеграла следует расходимость исходного ряда.
Теперь рассмотрим знакопеременные ряды.
Знакопеременным называется ряд
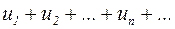 , (4)
, (4)
если среди его членов есть как положительные, так и отрицательные.
Составим ряд из абсолютных значений ряда (4):
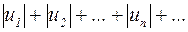 (5)
(5)
Если ряд (5) сходится, то ряд (4) тоже сходится и называется абсолютно сходящимся.
Из расходимости ряда (5) не следует расходимость ряда (4).
Если ряд (5) расходится, а ряд (4) сходится, то ряд (4) называется сходящимся условно.
Ряд (5) является знакоположительным рядом и вопрос о его сходимости решается с помощью признаков, рассмотренных ранее.
Частным случаем знакопеременного ряда является знакочередующийся ряд.
Знакочередующимся называется ряд, члены которого поочередно имеют то положительный, то отрицательный знаки (т.е. общий член ряда 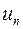 можно представить в виде
можно представить в виде 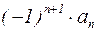 ):
):
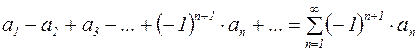 , (6)
, (6)
где 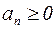 для любого
для любого 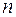 .
.
Для решения вопроса о сходимости знакочередующегося ряда используют признак сходимости Лейбница.
Признак сходимости Лейбница. Если для знакочередующегося ряда (6) выполнены условия:
1. 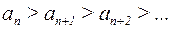 (начиная с некоторого n),
(начиная с некоторого n),
2. 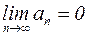 ,
,
то ряд (6) сходится.
Пример 9. Исследовать сходимость ряда 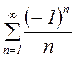 .
.
Решение: Это знакочередующийся ряд c 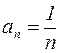 , для которого выполнены условия признака сходимости Лейбница:
, для которого выполнены условия признака сходимости Лейбница: 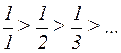 и
и 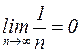 , поэтому ряд сходится. Он сходится условно, т.к. ряд, составленный из абсолютных значений, является гармоническим
, поэтому ряд сходится. Он сходится условно, т.к. ряд, составленный из абсолютных значений, является гармоническим 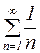 , который расходится.
, который расходится.
Пример 10. Исследовать сходимость ряда 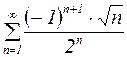 .
.
Решение: Можно, как в предыдущем примере, сначала применить признак Лейбница и, убедившись в сходимости ряда, исследовать эту сходимость (абсолютная или условная сходимость). А можно сразу рассмотреть ряд, составленный из абсолютных значений 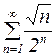 . Если такой ряд сходится, то мы сразу получим ответ, а если он расходится, то придется применить признак Лейбница, чтобы установить расходится ли исходный знакочередующийся ряд, или он сходится условно.
. Если такой ряд сходится, то мы сразу получим ответ, а если он расходится, то придется применить признак Лейбница, чтобы установить расходится ли исходный знакочередующийся ряд, или он сходится условно.
Поступим вторым способом. Применим к ряду 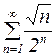 признак сходимости Даламбера:
признак сходимости Даламбера:
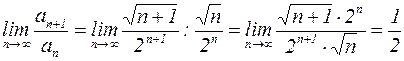 < 1,
< 1,
следовательно, этот ряд сходится, поэтому исходный ряд сходится абсолютно.
Теперь рассмотрим функциональные ряды.
Функциональным называется ряд
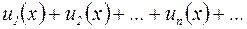 ,
,
членами которого являются зависящие от 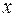 функции.
функции.
Множество значений аргумента 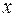 , при которых ряд сходится, называется областью сходимости ряда.
, при которых ряд сходится, называется областью сходимости ряда.
Частным случаем функционального ряда является степенной ряд:
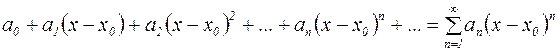 , (7)
, (7)
где 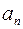 и
и  – вещественные числа.
– вещественные числа.
Для ряда (7) существует такой интервал, называемый интервалом сходимости, 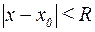 с центром в точке
с центром в точке 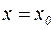 , внутри которого ряд (7) сходится абсолютно, а при
, внутри которого ряд (7) сходится абсолютно, а при 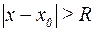 ряд расходится. Число
ряд расходится. Число 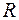 называют радиусом сходимости степенного ряда. Радиус сходимости
называют радиусом сходимости степенного ряда. Радиус сходимости 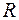 в частном случае может быть равен 0 или
в частном случае может быть равен 0 или 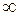 . На концах интервала сходимости степенной ряд может как сходиться, так и расходиться.
. На концах интервала сходимости степенной ряд может как сходиться, так и расходиться.
Для выяснения вопроса о сходимости ряда на концах интервала сходимости достаточно применить к ряду известные признаки сходимости, считая 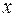 фиксированным и равным
фиксированным и равным 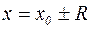 .
.
Пример 11. Найти область сходимости ряда 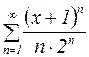 .
.
Решение: Так каквнутри интервала сходимости ряд сходится абсолютно, применим к ряду, составленному из абсолютных величин членов исходного ряда, признак сходимости Даламбера и рассмотрим предел:
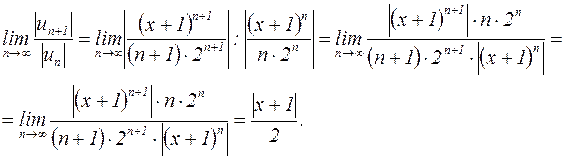
Запишем 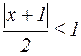 (условие сходимости ряда по признаку Даламбера) и найдем такие значения х, при которых это условие выполняется:
(условие сходимости ряда по признаку Даламбера) и найдем такие значения х, при которых это условие выполняется:
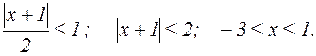
Итак, мы получили интервал сходимости: 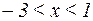 . Исследуем сходимость на концах этого интервала.
. Исследуем сходимость на концах этого интервала.
При х = -3 получаем числовой ряд:
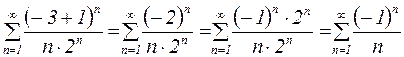 .
.
Это знакочередующийся ряд, который сходится по признаку Лейбница (см. пример 9).
При х = 1 получаем гармонический ряд:
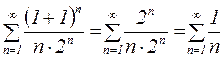 ,
,
который расходится.
Окончательный ответ: ряд сходится при 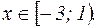
Если 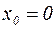 , то степенной ряд имеет вид:
, то степенной ряд имеет вид:
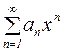 .
.
Пример 12. Определить область сходимости ряда 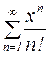 .
.
Решение: Рассмотрим предел:
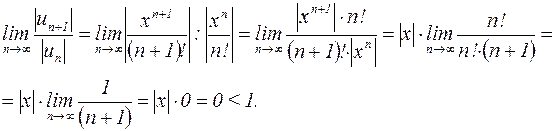
Мы получили результат, меньший единицы при всех значениях 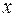 , поэтому область сходимости ряда:
, поэтому область сходимости ряда: 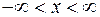 .
.
Требования к оформлению контрольной работы:
1. Работа выполняется в тетради со свободными полями для замечаний рецензента или на листах формата А4 в скоросшивателе.
2. На обложке должны быть указаны фамилия и инициалы студента, номер зачетной книжки, шифр, номер специальности, срок обучения, название дисциплины.
3. Контрольная работа должна содержать все задачи своего варианта, расположенные в порядке, указанном в задании. Перед решением каждой задачи должны приводиться ее условия.
4. Решение следует излагать подробно и аккуратно, делая необходимые объяснения и иллюстрации.
5. В случае получения от рецензента незачтенной работы следует исправить все отмеченные ошибки, внести необходимые исправления и прислать работу для повторной проверки. Рекомендуется при выполнении работы оставлять в конце тетради несколько чистых листов для внесения возможных исправлений после ее рецензирования.
6. Контрольную работу следует сдать не позже установленного срока (уточнить на кафедре высшей математики).
Список литературы:
1. Акимов А.В., Брыжина Э.Ф., Полозенко Н.А. Задачи и упражнения по аналитической геометрии и линейной алгебре: Учеб.-метод. пособие. – СПб.: СПбГИЭУ, 2002. – 72с.
2. АКИМОВ А.В., ГАЛИЛЕЕВ М.М., МОИСЕЕНКО Т.С. Математика для экономистов. Часть 1. Учебное пособие, СПбГИЭУ, 2002.
3. Брыжина Э.Ф., Линьков А.М., Митасов Е.В. Высшая математика. Элементы линейной алгебры: Методические указания к контрольной работе №1 для студентов 1 курса заочного и вечернего отделений всех специальностей. /ЛИЭИ – Л.,1990.
4. ДАНКО П.Е., ПОПОВ А.Г., КОЖЕВНИКОВА Т.Я. Высшая математика в упражнениях и задачах. М.: Высшая школа, 1986.
5. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1965–1975.
6. Карасев А.И. Курс высшей математики для экономических вузов. М:Высшая школа, 1982.
7. КОЛЕСНИКОВ А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: Инфра-М, 1997.
8. КРЕМЕР Н.Ш., ПУТКО Б.А., ТРИШИН Н.М., ФРИДМАН Н.М. Высшая математика для экономистов. М.: Банки и биржи, ЮНИТИ, 1997.
9. МИТАСОВ Е.В., ПРОНИН Л.Н., РОЖКОВ Ю.С., ТЕТЕРИН И.Ю. Дифференциальное исчисление функций одной и нескольких переменных. Учебное пособие, СПбГИЭУ, 2001.
10. ШИПАЧЕВ В.С. Высшая математика. М.: Высшая школа, 1998.
11. Математический анализ: Метод. указ. к изучению дисциплины и выполнению контр. работ №1,2 для студ. заоч. формы обуч./ Сост. В.Н. Ассаул, А.М. Васильев, Т.Н. Зауличева, А.В. Соколова – СПб.: СПбГИЭУ, 2005. – 70с.
12. Сборник задач по высшей математике для экономистов: Учебное пособие /Под ред. В.И. Ермакова – М.: ИНФРА– М, 2003. – 575с. – (Серия «Высшее образование»).
Приложение 1.
 2015-02-04
2015-02-04 919
919








