Линейное уравнение первого порядка имеет вид:
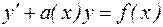
Решить линейное дифференциальное уравнение первого порядка можно с помощью введения двух новых искомых функций 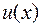 и
и 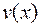 , положив
, положив 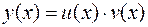 , и дополнительного условия на одну из них, выбираемую произвольно. Рассмотрим применение этого метода на следующем примере.
, и дополнительного условия на одну из них, выбираемую произвольно. Рассмотрим применение этого метода на следующем примере.
Пример 4. Решить дифференциальное уравнение
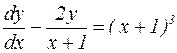 .
.
Решение: Будем искать решение в виде: 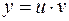 ;
;
Тогда 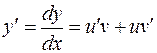 ; Подставляя выражения для искомой функции и ее производной в рассматриваемое дифференциальное уравнение, получим:
; Подставляя выражения для искомой функции и ее производной в рассматриваемое дифференциальное уравнение, получим:
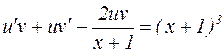 , или
, или
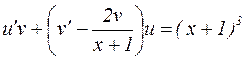 . (7)
. (7)
Поскольку одну из функций 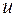 или
или 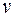 мы вправе выбрать произвольно, выберем ее так, чтобы выполнялось условие:
мы вправе выбрать произвольно, выберем ее так, чтобы выполнялось условие: 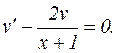 Тогда уравнение (7) запишется в виде:
Тогда уравнение (7) запишется в виде: 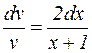 . Это уравнение легко интегрируется:
. Это уравнение легко интегрируется: 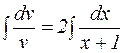 ;
; 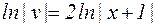 .
.
Произвольную постоянную здесь можно положить равной нулю, так как мы выбираем частное решение. Тогда 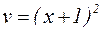 .
.
После подстановки 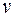 в исходное уравнение получим (при
в исходное уравнение получим (при 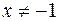 ):
):
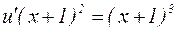 ;
; 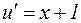 ;
; 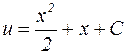 .
.
Таким образом, 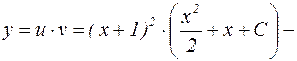 искомое общее решение.
искомое общее решение.
4. Уравнение Бернулли.
Уравнением Бернулли называется уравнение следующего вида:
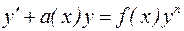 . (8)
. (8)
Это уравнение отличается от линейного уравнения множителем 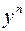 в правой части. Здесь
в правой части. Здесь 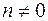 и
и 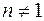 , так как в этих случаях уравнение (8) превращается в линейное уравнение.
, так как в этих случаях уравнение (8) превращается в линейное уравнение.
Уравнение Бернулли, как и линейное уравнение, решается с помощью представления этой функции в виде 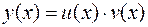 .
.
Пример 5. Решить уравнение:
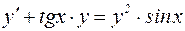 . (9)
. (9)
Решение: Это уравнение Бернулли и 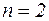 . Положим
. Положим 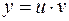 . Тогда уравнение (9) запишется в виде:
. Тогда уравнение (9) запишется в виде:
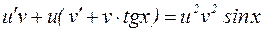 . (10)
. (10)
Будем искать функцию 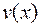 как решение уравнения:
как решение уравнения:
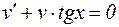 .
.
Тогда 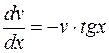 и
и 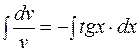 . Вычисляя интегралы, получим:
. Вычисляя интегралы, получим:
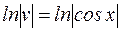 ;
;
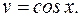
Подставляя полученное выражение в (10), получим:
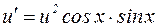 .
.
Разделяя переменные и интегрируя, получим:
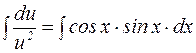 .
.
Выполняя интегрирование, приходим к выражению:
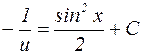 , или
, или 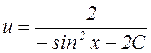 .
.
Окончательно получаем: 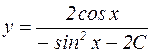 .
.
Дифференциальные уравнения второго порядка.
Дифференциальное уравнение второго порядка имеет вид:
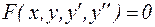 . (11)
. (11)
Если уравнение (11) может быть разрешено относительно второй производной, то оно записывается в виде:
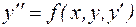 .
.
Задача Коши для дифференциального уравнения второго порядка состоит в нахождении частного решения, удовлетворяющего начальным условиям:
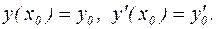
Рассмотрим основные виды дифференциальных уравнений второго порядка.
1. Дифференциальные уравнения, допускающие понижение порядка.
Некоторые дифференциальные уравнения с помощью замены переменных приводятся к уравнениям меньшего порядка, то есть допускают понижение порядка, что упрощает их решение. Применительно к уравнениям второго порядка это позволяет свести задачу к решению дифференциальных уравнений первого порядка.
Рассмотрим основные типы таких уравнений, имея в виду, что применяемые методы пригодны и для уравнений более высокого порядка.
а) Простейшее дифференциальное уравнение второго порядка.
Уравнение такого типа имеет вид:
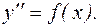 (12)
(12)
Поскольку правая часть уравнения (12) не зависит от 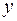 и
и 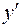 , общее решение может быть найдено непосредственным интегрированием левой и правой частей уравнения. После первого интегрирования получаем:
, общее решение может быть найдено непосредственным интегрированием левой и правой частей уравнения. После первого интегрирования получаем:
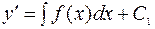 .
.
Повторное интегрирование приводит к общему решению:
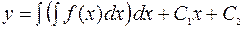 , (13)
, (13)
где 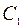 и
и 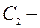 постоянные интегрирования.
постоянные интегрирования.
Пример 6. Найти решениедифференциального уравнения
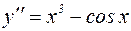 .
.
Решение: После первого интегрирования уравнения получим:
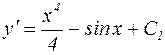
После повторного интегрирования имеем:
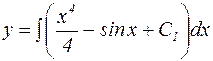
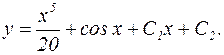
б) Дифференциальное уравнение, не содержащее искомой функции.
Уравнение такого типа имеет вид:
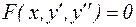 . (14)
. (14)
Введем новую функцию 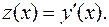 Тогда
Тогда 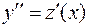 . С учетом этих соотношений уравнение (14) перепишется в виде:
. С учетом этих соотношений уравнение (14) перепишется в виде:
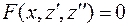 .
.
Получено уравнение первого порядка. Его решение ищется с помощью методов, изложенных выше. Пусть 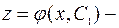 решение этого уравнения. Поскольку
решение этого уравнения. Поскольку 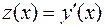 , приходим к уравнению
, приходим к уравнению 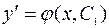 , которое легко интегрируется.
, которое легко интегрируется.
Пример 7. Решить задачу Коши:
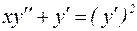 ,
, 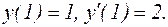
Решение: Положим 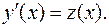 Так как
Так как 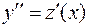 , дифференциальное уравнение принимает вид:
, дифференциальное уравнение принимает вид:
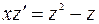 .
.
Это уравнение с разделяющимися переменными. Проинтегрируем его.
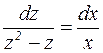 ,
, 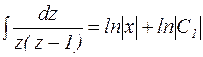 .
. 
Вычисляя интеграл в левой части последнего уравнения, получаем:
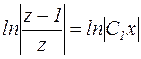 ,
, 
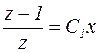 .
.
Из последнего уравнения находим 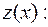
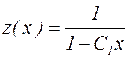 . Возвращаясь к переменной
. Возвращаясь к переменной 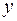 , получаем:
, получаем:
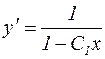 .
.
Определим постоянную интегрирования 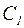 , используя одно из условий задачи Коши:
, используя одно из условий задачи Коши: 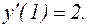 Получаем:
Получаем:
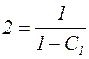 , то есть
, то есть 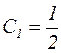 .
.
Тогда уравнение для искомой функции 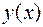 приобретает вид:
приобретает вид:
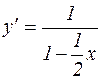 или
или 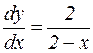 .
.
Последнее уравнение с разделяющимися переменными легко интегрируется:
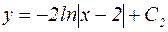 .
.
Найдем значение постоянной интегрирования 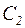 , используя первое из условий задачи Коши. Получаем:
, используя первое из условий задачи Коши. Получаем: 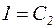 , то есть
, то есть 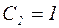 .
.
Теперь можно выписать решение задачи Коши:
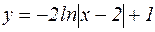 .
.
в) Дифференциальное уравнение, не содержащее независимой переменной.
Уравнение такого типа выглядит следующим образом:
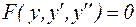 . (15)
. (15)
Вместо функции 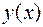 введем в рассмотрение новую функцию
введем в рассмотрение новую функцию 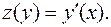 Тогда по правилу дифференцирования сложной функции получаем:
Тогда по правилу дифференцирования сложной функции получаем: 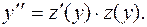
Подстановка этих соотношений в уравнение (15) превращает его в уравнении первого порядка относительно неизвестной функции:
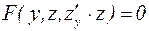 (16)
(16)
Пусть 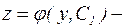 общее решение этого уравнения, найденное одним из методов решения дифференциальных уравнений первого порядка. Поскольку
общее решение этого уравнения, найденное одним из методов решения дифференциальных уравнений первого порядка. Поскольку 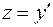 , последнее соотношение принимает вид
, последнее соотношение принимает вид 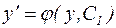 . Мы получили уравнение первого порядка с разделяющимися переменными, которое легко интегрируется.
. Мы получили уравнение первого порядка с разделяющимися переменными, которое легко интегрируется.
Пример 8. Найти общее решение дифференциального уравнения 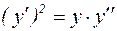 .
.
Решение: Положим 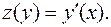 Тогда
Тогда 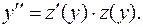 Подставим эти выражения в исходное уравнение:
Подставим эти выражения в исходное уравнение: 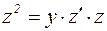 .
.
После разделения переменных получаем:
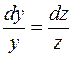 ,
, 
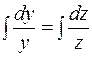 ,
, 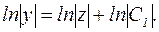
Из последнего уравнения находим: 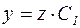 и
и 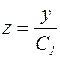 .
.
Так как 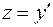 , получаем:
, получаем: 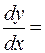
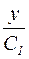 ,
, 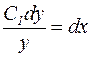 .
.
Отсюда 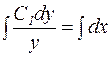 и
и 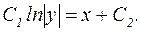
Мы получили общий интеграл исходного дифференциального уравнения в неявном виде:
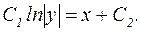
2. Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Дифференциальные уравнения этого типа имеет вид:
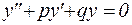 , (17)
, (17)
где 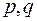 – постоянные числа.
– постоянные числа.
Будем искать решение уравнения (17) в виде 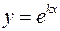 , где
, где 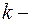 постоянное число. После подстановки этого выражения в (17) получим:
постоянное число. После подстановки этого выражения в (17) получим:
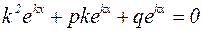 .
.
Поскольку 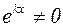 , должно выполняться квадратное уравнение:
, должно выполняться квадратное уравнение:
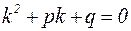 . (18)
. (18)
Это уравнение называется характеристическим уравнением для уравнения (17). В зависимости от величины его дискриминанта 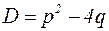 возможны три случая:
возможны три случая:
а) 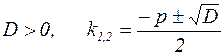 .
.
Можно показать, что общим решением в этом случае является комбинация двух линейно независимых решений, отвечающих двум различным корням характеристического уравнения:
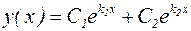 . (19)
. (19)
б) 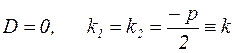 .
.
В этом случае общим решением будет:
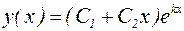 . (20)
. (20)
в) 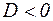 . В этом случае характеристическое уравнение имеет два комплексно-сопряженных корня:
. В этом случае характеристическое уравнение имеет два комплексно-сопряженных корня: 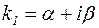 и
и 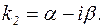
Общее решение записывается в следующем виде:
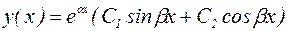 . (21)
. (21)
В формулах (19) – (21) 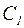 и
и 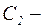 произвольные постоянные.
произвольные постоянные.
Пример 9. Решить дифференциальное уравнение:
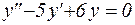 ;
;
Решение: Характеристическое уравнение принимает вид:
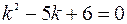 ;
;
Дискриминант положителен, уравнение имеет два различных корня: 
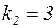 . Тогда, согласно (19), общее решение дифференциального уравнения записывается в виде:
. Тогда, согласно (19), общее решение дифференциального уравнения записывается в виде:
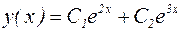 .
.
Пример 10. Решить дифференциальное уравнение: 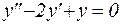 ;
;
Решение: Характеристическое уравнение 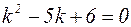 имеет один кратный корень
имеет один кратный корень 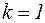 . В соответствии с (20) общее решение дифференциального уравнения записывается в виде:
. В соответствии с (20) общее решение дифференциального уравнения записывается в виде:
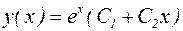 .
.
Пример 11. Решить дифференциальное уравнение:
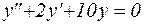 .
.
Решение: Дискриминант характеристического уравнения отрицателен, характеристическое уравнение имеет комплексные корни: 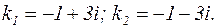 В этом случае формула (21) дает следующее общее решение дифференциального уравнения:
В этом случае формула (21) дает следующее общее решение дифференциального уравнения:
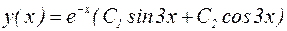 .
.
3. Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и специальной правой частью. Метод неопределенных коэффициентов.
Этот тип уравнений характеризуется наличием правой части, то есть имеет вид:
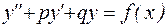 . (22)
. (22)
Можно доказать, что общее решение уравнения (22) представляется в виде:
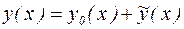 , (23)
, (23)
где 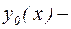 общее решение уравнения (22), а
общее решение уравнения (22), а 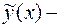 частное решение уравнения (22). Иными словами, общее решение линейного неоднородного уравнения есть сумма общего решения линейного однородного уравнения и одного из частных решений линейного неоднородного уравнения.
частное решение уравнения (22). Иными словами, общее решение линейного неоднородного уравнения есть сумма общего решения линейного однородного уравнения и одного из частных решений линейного неоднородного уравнения.
Отметим еще одно важное свойство решений линейных дифференциальных уравнений – принцип суперпозиции решений. Пусть правая часть линейного неоднородного дифференциального уравнения представляется в виде суммы двух (или более) функций:
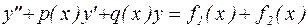 . (24)
. (24)
Тогда решение этого уравнения может быть представлено в виде 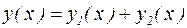 , где
, где 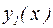 и
и 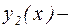 решения дифференциальных уравнений:
решения дифференциальных уравнений: 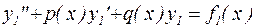 и
и 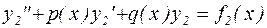 соответственно. Это означает, что, разбив правую часть линейного неоднородного дифференциального уравнения на сумму двух слагаемых, можно свести его решение к решению двух более простых дифференциальных уравнений.
соответственно. Это означает, что, разбив правую часть линейного неоднородного дифференциального уравнения на сумму двух слагаемых, можно свести его решение к решению двух более простых дифференциальных уравнений.
Заметим, что при формулировке принципа суперпозиции решений не требуется постоянство коэффициентов. Кроме того, этот принцип справедлив и для дифференциальных уравнений более высокого порядка.
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами (22), в котором правая часть имеет следующий вид:
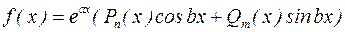 ,
,
где 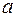 ,
, 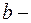 постоянные числа,
постоянные числа, 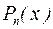 ,
, 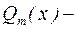 многочлены порядка
многочлены порядка 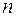 и
и 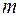 .
.
Такие уравнения называют уравнениями со специальной правой частью, и для нахождения их частного решения можно применить метод Эйлера. Согласно этому методу, частное решение ищется в следующем виде:
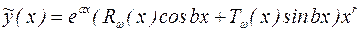 . (25)
. (25)
В правой части равенства (25) 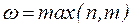 , а
, а 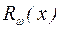 и
и 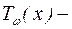 многочлены степени
многочлены степени 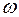 с неопределенными коэффициентами.
с неопределенными коэффициентами.
Степень множителя 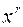 определяется по следующему правилу: если контрольное число
определяется по следующему правилу: если контрольное число 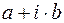 (комплексное при
(комплексное при 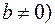 не совпадает ни с одним из корней характеристического уравнения (23), то
не совпадает ни с одним из корней характеристического уравнения (23), то 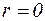 . Если контрольное число совпадает с одним из корней характеристического уравнения, то
. Если контрольное число совпадает с одним из корней характеристического уравнения, то 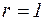 . Наконец, если контрольное число совпадает с корнем характеристического уравнения и этот корень кратный, то
. Наконец, если контрольное число совпадает с корнем характеристического уравнения и этот корень кратный, то 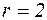 . Очевидно, что последний случай возможен только при
. Очевидно, что последний случай возможен только при 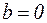 , так как кратный корень может быть только вещественным (действительным).
, так как кратный корень может быть только вещественным (действительным).
Для определения неопределенных коэффициентов в многочленах 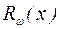 и
и 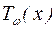 следует подставить выражение (25) в уравнение (22), предварительно найдя его производные
следует подставить выражение (25) в уравнение (22), предварительно найдя его производные 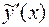 и
и 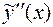 . Неопределенные коэффициенты находятся из системы линейных алгебраических уравнений, к которым сведется уравнение (22) после подстановки в него выражения (25).
. Неопределенные коэффициенты находятся из системы линейных алгебраических уравнений, к которым сведется уравнение (22) после подстановки в него выражения (25).
Пример 12. Решить дифференциальное уравнение:
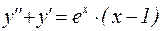 .
.
Решение: Характеристическое уравнение для однородного дифференциального уравнения имеет вид: 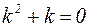 . Его корни
. Его корни 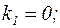
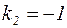 . Общее решение однородного уравнения записывается в форме:
. Общее решение однородного уравнения записывается в форме: 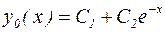 , где
, где 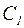 и
и 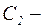 произвольные постоянные.
произвольные постоянные.
Будем искать частное решение неоднородного уравнения в виде (25). По условиям примера 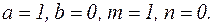 Контрольное число равно единице и не совпадает с корнями характеристического уравнения. Поэтому
Контрольное число равно единице и не совпадает с корнями характеристического уравнения. Поэтому 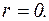 Таким образом, формула (25) дает:
Таким образом, формула (25) дает: 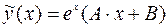 . Найдем производные
. Найдем производные 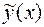 :
:
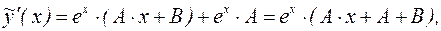
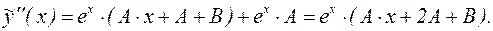
Подставим эти выражения в дифференциальное уравнение:
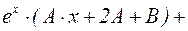
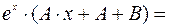
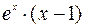 .
.
Сокращая обе части уравнения на 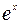 и приводя подобные, получаем:
и приводя подобные, получаем:
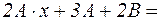
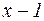 .
.
Последнее равенство должно выполняться для произвольных значений 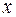 , что возможно лишь при выполнении следующих условий:
, что возможно лишь при выполнении следующих условий:
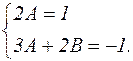
Решая систему уравнений, находим: 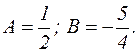
Следовательно, 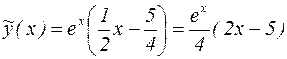 и общее решение рассматриваемого дифференциального уравнения принимает вид:
и общее решение рассматриваемого дифференциального уравнения принимает вид:
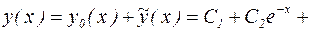
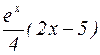 .
.
Пример 13. Найти общее решение дифференциального уравнения:
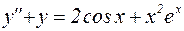 .
.
Решение: Характеристическое уравнение для однородного дифференциального уравнения 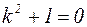 имеет два комплексно-сопряженных корня:
имеет два комплексно-сопряженных корня: 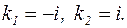 Общее решение однородного уравнения записывается в виде:
Общее решение однородного уравнения записывается в виде: 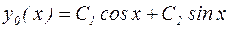 , где
, где 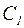 и
и 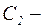 произвольные постоянные.
произвольные постоянные.
Найдем частное решение неоднородного уравнения. Заметим, что правая часть уравнения – сумма двух слагаемых, каждое из которых может быть представлено в виде (25). Поэтому, в соответствии с принципом суперпозиции решений, частное решение неоднородного уравнения будем искать в виде:
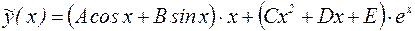 .
.
Найдем производные функции 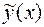 :
:
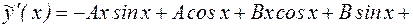
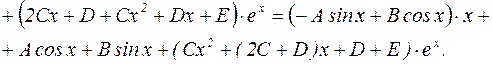
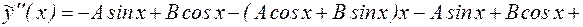
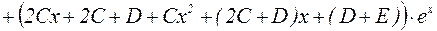 .
.
Подставим эти выражения в исходное уравнение:
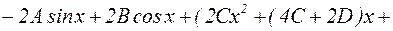
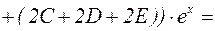
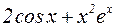 .
.
Выполнение этого уравнения при произвольных значениях 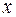 возможно только в том случае, когда коэффициенты при функциях
возможно только в том случае, когда коэффициенты при функциях 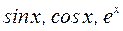 в левой и правой частях уравнения будут одинаковы. Это условие приводит к системе уравнений:
в левой и правой частях уравнения будут одинаковы. Это условие приводит к системе уравнений:
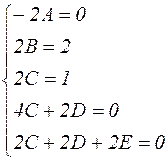
Ее решение: 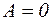 ;
; 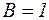 ;
; 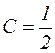 ;
; 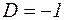 ;
; 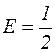 .
.
В окончательном виде получаем общее решение неоднородного дифференциального уравнения:
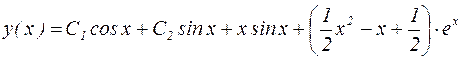 .
.
4. Линейное неоднородное дифференциальное уравнение второго порядка с произвольными коэффициентами. Метод Лагранжа.
Рассмотрим метод нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с произвольными коэффициентами (постоянными или переменными) и правой частью любого вида. Это универсальный метод, его называют методом вариации произвольных постоянных, или методом Лагранжа.
Рассмотрим этот метод применительно к уравнению (22). Согласно этому методу сначала находят два линейно независимых решения 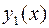 и
и 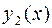 соответствующего однородного дифференциального уравнения. Частное решение неоднородного дифференциального уравнения ищется в виде их линейной комбинации, в которой произвольные постоянные
соответствующего однородного дифференциального уравнения. Частное решение неоднородного дифференциального уравнения ищется в виде их линейной комбинации, в которой произвольные постоянные 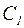 и
и 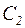 заменяются на неизвестные функции
заменяются на неизвестные функции 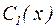 и
и 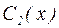 :
:
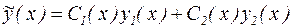 . (26)
. (26)
Подстановка этого выражения в неоднородное дифференциальное уравнение (22) приводит к следующему уравнению:
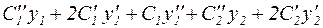
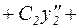
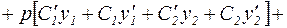
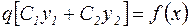 . (27)
. (27)
Перегруппируем слагаемые в (27):
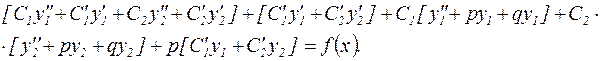 (28)
(28)
Рассмотрим подробнее уравнение (28). Так как функции 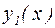 и
и 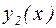 являются решениями однородного дифференциального уравнения (17), выражения в третьей и четвертой скобках в (28) тождественно равны нулю. Наложим на пока неопределенные функции
являются решениями однородного дифференциального уравнения (17), выражения в третьей и четвертой скобках в (28) тождественно равны нулю. Наложим на пока неопределенные функции 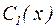 и
и 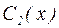 следующее условие:
следующее условие:
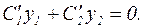 (29)
(29)
Тогда выражение в пятой скобке в (28) также окажется равным нулю. Продифференцируем обе части равенства (28):
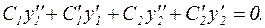
Это соотношение показывает, что и выражение в первой скобке в (28) тождественно равно нулю.
Таким образом, при условии (29) уравнение (28) сводится к следующему: 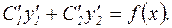 Иными словами, уравнение (28) равносильно системе уравнений:
Иными словами, уравнение (28) равносильно системе уравнений:
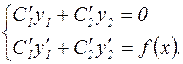 (30)
(30)
Поскольку определитель этой системы является вронскианом двух линейно независимых решений 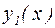 и
и 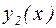 , и отличен от нуля, то система всегда имеет единственное решение.
, и отличен от нуля, то система всегда имеет единственное решение.
Решив систему уравнения (30), остается лишь найти 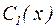 и
и 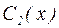 , то есть проинтегрировать полученные из (30) функции
, то есть проинтегрировать полученные из (30) функции 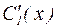 ,
, 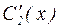 и подставить их в выражение для
и подставить их в выражение для 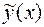 .
.
Пример 14. Найти решение дифференциального уравнения:
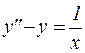 .
.
Решение: Это уравнение с постоянными коэффициентами, но его правая часть не имеет специального вида, допускающего применение метода неопределенных коэффициентов.
Поэтому для нахождения частного решения этого линейного неоднородного дифференциального уравнения воспользуемся методом вариации произвольных постоянных. Сначала найдем решение соответствующего однородного дифференциального уравнения:
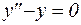 .
.
Характеристическое уравнение 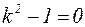 имеет корни
имеет корни 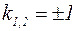 , и общее решение записывается в виде:
, и общее решение записывается в виде:
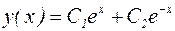 .
.
Частное решение исходного неоднородного уравнения ищем в виде:
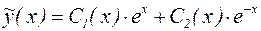 .
.
Система (30) приобретает вид:
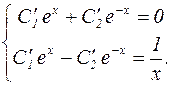
Отсюда находим:
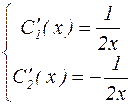 и
и 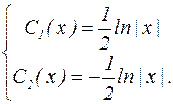
В итоге получаем: 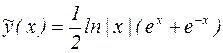 .
.
Общее решение рассматриваемого уравнения принимает вид:
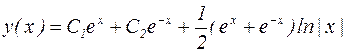 .
.
 2015-02-04
2015-02-04 1164
1164
