Площадь 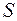 криволинейной трапеции, ограниченной графиком неотрицательной функции
криволинейной трапеции, ограниченной графиком неотрицательной функции 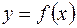 , осью
, осью 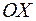 и прямыми
и прямыми 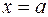 и
и 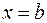 (рис.2) вычисляется по формуле:
(рис.2) вычисляется по формуле:
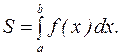
Если (условие неотрицательности функции нарушается) часть графика функции 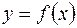 находится под осью
находится под осью 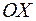 (рис.3), то площадь заштрихованной фигуры равна:
(рис.3), то площадь заштрихованной фигуры равна:
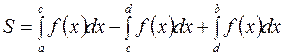 .
. 
Пусть фигура ограничена графиками двух функций:
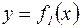 ,
, 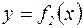 и
и 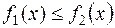 ,
, 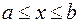 (рис. 4).
(рис. 4).
Тогда ее площадь вычисляется по формуле:
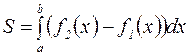 .
.
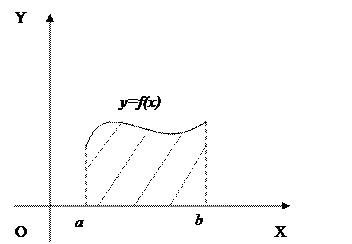
Рис.2
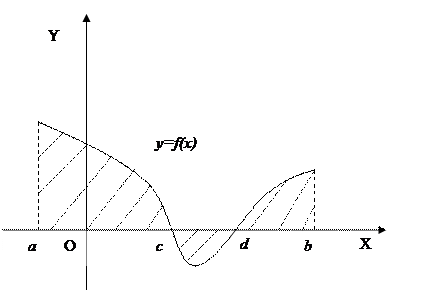
Рис. 3
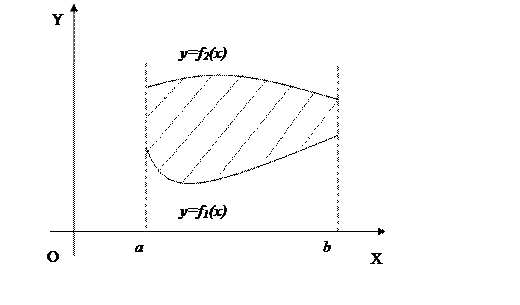
Рис. 4
Пример 4. Вычислить площадь фигуры, ограниченной прямой 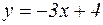 и параболой
и параболой 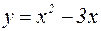 .
.
Решение: Построим графики прямой и параболы (рис. 5).
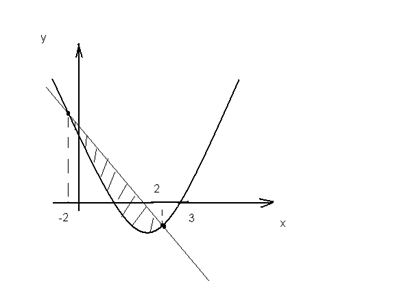
Рис. 5.
Найдем точки пересечения параболы и прямой:
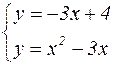
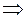
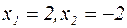 .
.
Тогда получим:
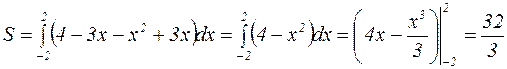 .
.
 2015-02-04
2015-02-04 356
356








