Системы массового обслуживания с отказами и неоднородными потоками

Постановка задачи. На вход n -канальной СМО поступает неоднородный простейший поток с суммарной интенсивностью λ_Σ, причем

λ_Σ = ,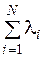

где λ _i – интенсивность заявок в i -м источнике.

Так как поток заявок рассматривается как суперпозиция требований от различных источников, то объединенный поток с достаточной для практики точностью [23] можно считать пуассоновским для N = 5...20 и λ _i ≈ λ _{i +1} (i Î1, N). Интенсивность обслуживания одного прибора распределена по экспоненциальному закону и равна μ = 1/ t. Обслуживающие приборы для обслуживания заявки соединяются последовательно, что равносильно увеличению времени обслуживания во столько раз, сколько приборов объединяется для обслуживания:

t _обс = kt, μ_обс = 1 / kt = μ/ k,

где t _обс – время обслуживания заявки; k – число обслуживающих приборов; μ_обс – интенсивность обслуживания заявки.

В рамках принятых в главе 2 допущений состояние СМО представим в виде вектора 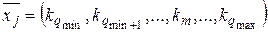, где k_m – число заявок в системе, каждая из которых обслуживается m приборами; L = q _max – q _min+1 – число входных потоков.

Тогда количество занятых и свободных приборов (n _зан(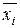), n _св(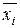)) в состоянии 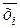определяется следующим образом:

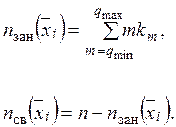
Из состояния 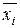система может перейти в любое другое состояние 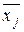. Так как в системе действует L входных потоков, то из каждого состояния потенциально возможно L прямых переходов. Однако из-за ограниченности ресурсов системы не все эти переходы осуществимы. Пусть СМО находится в состоянии 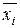и приходит заявка, требующая m приборов. Если m ≤ n _св(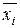), то заявка принимается на обслуживание и система переходит в состояние 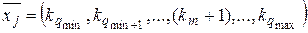с интенсивностью λ _m. Если же заявка требует приборов больше, чем имеется свободных, то она получит отказ в обслуживании, а СМО останется в состоянии 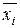. Если в состоянии 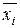находятся заявки, требующие m приборов, то каждая из них обслуживается с интенсивностью m/ m, а общая интенсивность обслуживания таких заявок (μ _m) определяется как μ _m = k_m μ / m. При завершении обслуживания одной из заявок система перейдет в состояние, в котором соответствующая координата имеет значение, на единицу меньшее, чем в состоянии 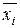, 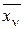= 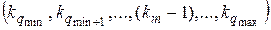, т.е. произойдет обратный переход. На рис. 3.9 представлен пример векторной модели СМО для n = 3, L = 3, q _min = 1, q _max = 3, P (m) = 1/3, λ_Σ = λ, интенсивность обслуживания прибора – μ.

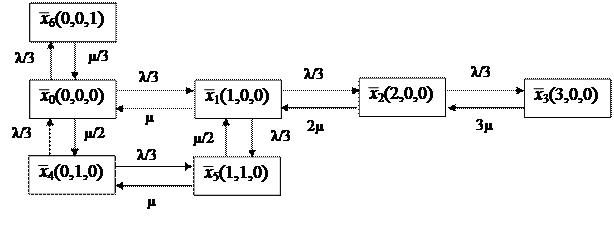
Рис. 3.9. Пример графа векторной модели СМО с отказами в обслуживании

Итак, каждое состояние 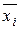характеризуется числом обслуживаемых заявок определенного типа. Например, в состоянии 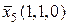обслуживается одна заявка одним прибором и одна заявка двумя приборами. В этом состоянии все приборы заняты, следовательно, возможны лишь обратные переходы (приход любой заявки в этом состоянии приводит к отказу в обслуживании). Если раньше закончилось обслуживание заявки первого типа, то система перейдет в состояние 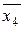(0,1,0) с интенсивностью μ, если же раньше закончилось обслуживание заявки второго типа, то система перейдет в состояние 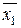(0,1,0) с интенсивностью μ/2.

По графу состояний с нанесенными интенсивностями переходов составляется система линейных алгебраических уравнений. Из решения этих уравнений находятся вероятности Р (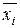), по которым определяется характеристика СМО.

Рассмотрим нахождение Р _отк (вероятность отказа в обслуживании).

,

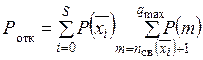где S – число состояний графа векторной модели СМО; Р (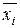) – вероятность нахождения системы в состоянии .

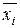Число состояний согласно [11] определяется следующим образом:

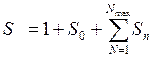, (3.22)

где

;

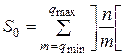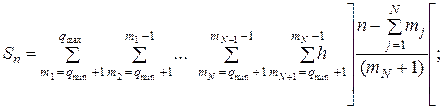
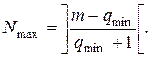
Определим число состояний векторной модели СМО по (3.22) для примера, представленного на рис. 3.9.

.

.

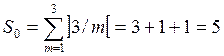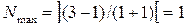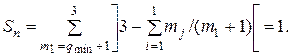
Следовательно, S = 1 + 5 + 1 = 7.

Для реализации реальных требований к обслуживающим приборам необходимо достаточно большое число n (40,..., 50), а запросы на число обслуживающих приборов заявки на практике лежат в пределах 8–16. При таком соотношении приборов и запросов предложенный путь нахождения вероятностей становится чрезвычайно громоздким, т.к. векторная модель СМО имеет большое число состояний S (50) = 1790, S (60) = 4676, S (70) = = 11075, а размер матрицы коэффициентов системы алгебраических уравнений пропорционален квадрату S [24], что требует большого объема памяти ЭВМ и значительных затрат машинного времени. Стремление снизить объем вычислений стимулировало поиск рекуррентных возможностей расчета Р (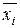) на основе мультипликативных форм представления вероятностей состояний. В работе [11] представлен подход к расчету Р ():

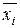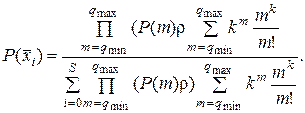(3.23)

Использование предложенного в работе [11] критерия эквивалентности глобального и детального балансов цепей Маркова позволяет снижать размерность задачи и выполнять вычисления на ЭВМ средней мощности, используя рекуррентность вычислений. Кроме того, имеется возможность:

– произвести расчет для любых значений n;

– ускорить расчет и снизить затраты машинного времени.

Аналогичным образом могут быть определены и другие характеристики системы.