Системы массового обслуживания с отказами и полной взаимопомощью между каналами

Постановка задачи. На вход n -канальной СМО поступает простейший поток заявок с интенсивностью λ. Интенсивность простейшего потока обслуживает каждого канала равна μ. Если заявка застает все каналы свободными, то она принимается на обслуживание и обслуживается всеми n каналами одновременно. Предполагается, что такое обслуживание возможно и при этом приборы обслуживают заявку параллельно, что равносильно увеличению в n раз интенсивности обслуживания (n m). После окончания обслуживания все n каналов освобождаются одновременно.

Если вновь прибывшая заявка застает в системе одну заявку, то она принимается на обслуживание. В этом случае часть каналов продолжает обслуживать первую заявку, а остальные каналы приступают к обслуживанию вновь прибывшей заявки. Распределение каналов по заявкам может производиться любым образом. Если прибывшая новая заявка застает в системе две обслуживаемые заявки и n > 2, то каналы распределяются по всем трем заявкам, и т.д.

Если вновь прибывшая заявка застает в системе k заявок (k = 1,2,..., n –1), то она принимается к обслуживанию и все n каналов перераспределяются произвольным образом между k + 1 заявками, но так, чтобы все каналы участвовали в обслуживании.

Если вновь прибывшая заявка застает в системе n заявок, то она получает отказ и не обслуживается. Попавшая на обслуживание заявка обслуживается до конца (заявки «терпеливые»).

Если обслуживание какой-либо заявки окончено, то освободившаяся группа каналов присоединяется к обслуживанию остальных заявок, находящихся в системе. Таким образом, при наличии в системе хотя бы одной заявки все n каналов все время будут заняты.

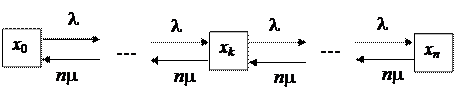Граф состояний такой системы приведен на рис. 3.7.

Рис. 3.7. Граф состояний СМО с отказами и полной

взаимопомощью между каналами

Для пуассоновских потоков и стационарного режима СМО будет описываться следующей системой алгебраических уравнений:

0 = –λ Р ₀ + n μ Р ₁,

.………………

0 = –(λ + n μ) Р_k + λ Р_{k –1} + n μ Р_{k +1} (k = 1,2,..., n –1),

……………....

0 = λ Р_{n –1} – n μ Р_n.

Используя тот же подход, что и в § 3.4.1, получим

u_i = –λ P_{i –1}+ n μ Р_i (i = 1,2,..., n),

u ₁= 0,

…...…

u_{k +1} – u_k = 0 (k = 1,2,..., n –1),

…..…

u_n = 0,

откуда

.

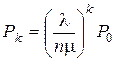Введя обозначение 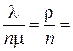χ и используя нормировочное условие, получим

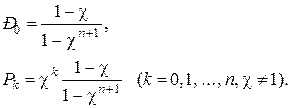
Это выражение справедливо для любых значений χ ≠ 1. При χ = 1 имеет место неопределенность, раскрывая которую, получим

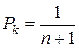(k = 0,1,..., n, χ = 1),

т.е. все состояния будут равновероятными.

Определим основные параметры системы.

Вероятность обслуживания заявки определяется из выражения

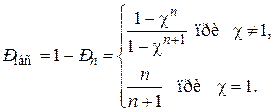
Найдем среднее число заявок 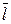, находящихся в системе:

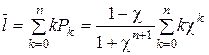. (3.21)

Для вычисления суммы, входящей в выражение (3.21), воспользуемся методом дифференцирования рядов [9] и получим

.

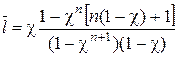При χ = 1 .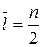

Среднее число занятых каналов 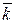определяется так:

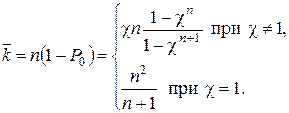
Для этой системы вероятность того, что любой отдельный канал будет занят, равна вероятности того, что все каналы будут заняты.

.

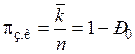Среднее время простоя

.

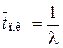Среднее время занятости канала

.

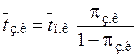Аналогичным образом могут быть определены и другие характеристики системы.