Задача 1. По следующим данным определите средний стаж рабочего (табл.4.5):
Таблица 4.5
| Общий стаж работы, лет | до 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25 и более | Итого |
| Число рабочих |
Решение. Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения - интервальный, причем первый и последний интервал - открытые.
Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала
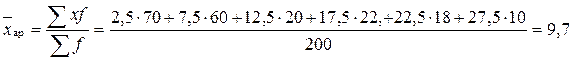 .
.
Задача 2. Все частоты уменьшились в два раза, а все варианты увеличились на две единицы. Что произойдет со средней?
Решение. Согласно свойствам средней арифметической, если все частоты ряда уменьшить или увеличить в одинаковое количество раз, то средняя не изменится, т.е. с точки зрения частот - средняя не изменится. Если все варианты увеличить или уменьшить на одно и то же число, то и средняя изменится на это же число. В нашем случае средняя увеличится на две единицы.
Задача 3. Двое рабочих в течение 8-часового рабочего дня изготовляют одни и те же детали. Первый из них тратит на изготовление детали 30 мин., второй - 40 мин. Вычислите среднюю затрату времени на изготовление одной детали.
Решение. В этой задаче явно даны только значения признака - затраты времени, а частоты, которыми является количество изготовленных каждым рабочим деталей, в явном виде не присутствуют. Однако произведения значений признака на частоты дает количество проработанного времени - 8 час. Так как произведения признака на частоту равны, то средняя определяется по формуле средней гармонической простой:
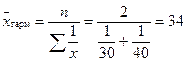 мин.
мин.
Задача 4. Автомобиль проехал 1000 км, из них 480 км он прошел со скоростью 60 км/час, 320 - со скоростью 80 км/час и 200 км - со скоростью 50 км/час. Определите среднюю скорость, с которой совершался рейс.
Решение. В этой задаче опять известны только значения признака, а значения частот (время) не даны, однако имеются данные о пройденном расстоянии, которое является произведением признака на частоту. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной:
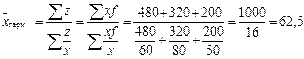 км/ч.
км/ч.
Задача 5. Определите среднегодовой темп роста выпуска продукции на заводе, если в 1990 г. было произведено продукции на 21,15 у.д.е., а в 1995 г. было запланировано произвести продукции на 35 у.д.е.
Решение. Для определения средних темпов роста применяется средняя геометрическая. Когда имеются данные о первом периоде (в нашем случае - выпуск продукции в 1990 г. на сумму 21,15 у.д.е.) и в последнем периоде (в задаче — выпуск продукции по плану в 1995 г. на сумму 35 у.д.е.), среднегодовой темп роста определяется по формуле:
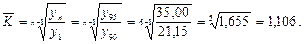
Задача 6. Определить моду и медиану по следующим данным (табл. 4.6):
Таблица 4.6
Распределение студентов заочного отделения по возрасту
| Возрастные группы | Число студентов | Накопленные частоты |
| до 20 лет | ||
| 20-25 | ||
| 25-30 | ||
| 30-35 | ||
| 35-40 | ||
| 40-45 | ||
| 45 лет и выше | ||
| Итого: |
Решение. Для определения моды определяем модальный интервал. Им является интервал 25-30 лет, так как его частота наибольшая (1054), тогда
Мо 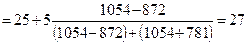 лет.
лет.
Для определения медианы тоже необходимо определить медианный интервал. Медианным интервалом является интервал 25-30, так как он является первым интервалом, накопленная частота которого превышает полусумму частот (3462: 2=1731). Тогда медиана определится как:
Ме 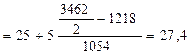 года.
года.
РАЗДЕЛ 5. ПОКАЗАТЕЛИ ВАРИАЦИИ И ДРУГИЕ ХАРАКТЕРИСТИКИ РЯДОВ РАСПРЕДЕЛЕНИЯ
5.1. Понятие о вариации
При изучении процессов и явлений общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующей отдельные единицы совокупности. Величина признака изменяется, колеблется под влиянием различных причин и условий. Чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.
Таблица 5.1
Дневная выработка рабочих двух бригад
| Номер бригады | Число рабочих | Дневная выработка деталей отдельных рабочих, шт. | Средняя дневная выработка |
| 75 90 78 82 93 86 | |||
| 65 122 84 70 105 58 |
Одна и та же средняя может характеризовать совокупность, в которой размеры вариации признака существенно отличаются друг от друга (табл.5.1). Как видно, средняя дневная выработка в обеих бригадах одинакова, хотя в первой бригаде средняя значительно меньше отличается от индивидуальных значений признака, чем во второй.
Следовательно, для всесторонней характеристики рядов распределения необходимы показатели, определяющие меру, степень колеблемости отдельных значений признака от средней, т.е. степень вариации, а также форму (тип) распределения, характеризующую ее закономерности.
5.2. Показатели вариации и способы их расчета
а) Размах вариации является наиболее простой мерой колеблемости значений признака и представляет собой разность между максимальным и минимальным значением признака: R = Х max - Х min.
Размах вариации имеет недостаток, проявляющийся в том, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость признака.
В связи с тем, что каждое индивидуальное значение признака отклоняется от средней на определенную величину, мерой вариации может служить средняя из отклонений каждой отдельной варианты от их средней.
Такими показателями являются среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
б) Среднее линейное отклонение представляет собой среднюю из абсолютных значений отклонений индивидуальных значений признаков от их средней:
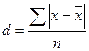 ;
; 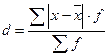 .
.
Недостаток среднего линейного отклонения в том, что оно берется без учета знака. Поэтому в статистике чаще используют дисперсию и среднее квадратическое отклонение.
в) Дисперсия и среднее квадратическое отклонение. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины
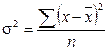 ;
; 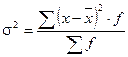 .
.
Дисперсия имеет очень большое значение в анализе. Однако ее применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому вычисляют среднее квадратическое отклонение, равное корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии
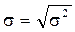 .
.
Сопоставление линейных или средних квадратических отклонений по нескольким совокупностям дает возможность определять степень их однородности в отношении того или иного признака. Чем меньше: R, d, σ2,σ, тем совокупность более однородна, тем более типичной будет средняя величина.
г) Коэффициент вариации. Так как дисперсия и среднее квадратическое отклонение характеризуют абсолютный размер отклонений, то представляет интерес сопоставить среднее квадратическое отклонение с его средней величиной. Такой показатель называется коэффициентом вариации
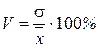 .
.
Если взять отношение среднего линейного отклонения к средней арифметической, то получим линейный коэффициент вариации 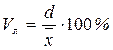 .
.
Отношение размаха вариации к средней арифметической называется коэффициентом осцилляции: 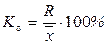 .
.
 2015-02-14
2015-02-14 31684
31684
