Задача 1. По следующим данным вычислить среднемесячные остатки материалов за полугодие (табл 8.1):
Таблица 8.1
| Дата | 1/1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 |
| Остатки на начало месяца, у.д.е. | 464.8 | 446.0 | 428.0 | 436.0 | 423.8 | 421.4 | 410.2 |
Решение. В нашей задаче даны остатки материалов на определенные моменты в ремени (1/1, 1/2, и т.д.), промежутки между которыми равны. В этом случае средняя исчисляется по формуле средней хронологического ряда:
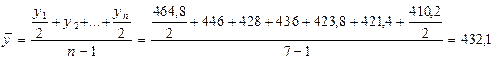 у.д.е.
у.д.е.
Задача 2. По следующим данным определите среднее поголовье коров по совхозу за год (табл 8.2):
Таблица 8.2
| Дата | 1.01.95 | 1.07.95 | 1.11.95 | 1.01.96 |
| Поголовье |
Решение. В задаче дано поголовье коров за определенный момент, даты, причем интервалы между датами не равны (6, 4 и 2 месяца). В таких случаях средняя хронологическая моментного ряда рассчитывается как средняя арифметическая взвешенная, где в качестве весов применяются отрезки времени между датами, к которым относятся парные средние смежные значения уровня. Определим прежде всего средние смежные значения уровней.
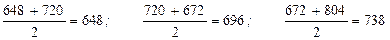 .
.
Взвесим их теперь на отрезке времени между датами
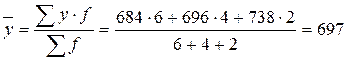 .
.
Задача 3. Производство продукции по предприятию за 1990 - 1994 гг. характеризуется следующими данными (табл. 8.3):
Таблица 8.3
| Годы | |||||
| Производство продукции, тыс.шт. |
Определить:
16.начальный, конечный и средний уровни ряда;
17.абсолютные приросты по годам, к 1990 г. и среднегодовой абсолютный прирост;
18.темп роста и прироста по годам и к 1990 г.;
19.абсолютное значение одного процента прироста;
20.среднегодовой темп роста и прироста за период 1990 - 1994 гг.
Решение.
1. Начальный уровень (величина первого члена ряда) - 4140, конечный - 5426. Средний уровень ряда определяется по формуле простой средней арифметической, так как ряд периодический
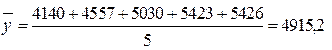 тыс. шт.
тыс. шт.
Вычисленные основные показатели данного динамического ряда сводим в таблицу 8.4.
2. Абсолютный прирост показывает, насколько изменился текущий уровень по сравнению с предыдущим или базисным и определяется как разность двух уровней
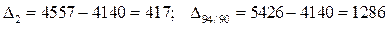 .
.
Среднегодовой абсолютный прирост исчисляется по формуле средней арифметической простой и равен
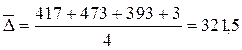 тыс. шт.
тыс. шт.
Среднегодовой абсолютный прирост можно вычислить и таким образом:
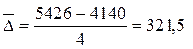 тыс.шт.
тыс.шт.
3. Темп роста показывает, во сколько раз текущий уровень больше предыдущего или базисного, и определяется как отношение двух уровней, выраженное в процентах:
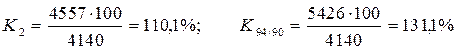 .
.
Темп прироста показывает, на сколько процентов увеличился текущий уровень по сравнению с текущим или базисным и определяется как разность соответствующего темпа роста и 100%:
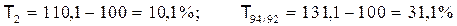 .
.
Абсолютное значение 1% прироста определяется как отношение абсолютного прироста к темпу прироста:
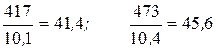 и т. д.
и т. д.
5. Среднегодовой темп роста рассчитывается по формуле средней геометрической
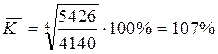 .
.
Среднегодовой темп прироста равен среднегодовому темпу роста минус 100%, т. е. 107% -100% = 7%
Таблица 8.4
| Год | тыс.шт. | Абсолютные приросты, тыс. шт. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. шт. | |||
| цепные | базисные | цепные | базис-ные | цеп-ные | базис-ные | |||
| - | - | - | - | - | - | - | ||
| 110,1 | 110,1 | 10,1 | 10,1 | 41,4 | ||||
| 110,4 | 121,5 | 10,4 | 21,5 | 45,6 | ||||
| 107,8 | 131,0 | 7,8 | 31,0 | 50,3 | ||||
| 100,06 | 131,1 | 0,06 | 31,1 | 54,2 |
Задача 4. Среднегодовой темп роста заработной платы рабочих завода за 1990-91 гг. составил 104%, а за 1992-1994 гг. -106%. Определить среднегодовой темп роста заработной платы на заводе за 1990 - 1994 гг.
Решение. Средняя из средних темпов роста за неодинаковые промежутки времени рассчитывается по формуле средней геометрической взвешенной, причем весами являются сами промежутки времени, следовательно:
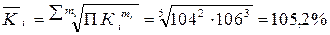 .
.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ТЕМЫ
ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ И ЭКЗАМЕНУ
21. Предмет и метод статистики.
22. Что такое закономерность? Динамические и статистические закономерности и их особенности.
23. Что такое статистическая совокупность, единица совокупности? Понятие вариации.
24. В чем сущность и значение закона больших чисел?
25.Какие науки являются теоретической основой статистики?
26.Чем объясняется расчленение статистической науки на отдельные отрасли? Почему изучение статистической науки начинается с общей теории статистики?
27. Сущность и виды учета.
28. На какие этапы подразделяется статистическое исследование?
29. Дайте определение статистического наблюдения. В чем его сущность?
30. Какие две организационные формы статистического наблюдения вы знаете?
31. Что такое объект наблюдения, единица наблюдения и единица совокупности?
32. Какое время в статистике называется объективным и в чем его отличие от субъективного?
33.Что такое критический момент?
34.Классификация видов и способов статистического наблюдения.
35. В чем состоит логический и арифметический контроль материалов статистического наблюдения?
36. Классификация ошибок наблюдения.
37. Случайные и систематические ошибки и их особенности.
38.Дайте понятие сводки.
39.Статистические группировки и их виды.
40.Общее понятие классификации, виды классификаций.
41. Какие признаки называются атрибутивными, а какие - количественными?
42. Что представляют собой ряды распределения и для чего они служат?
43. В чем отличие вариационного ряда от атрибутивного?
44. Что такое частоты, частости, варианты, объем ряда?
45. Как подразделяются вариационные ряды распределения?
46. Что такое полигон распределения, гистограмма распределения?
47. Что такое плотность распределения?
48. Что такое кумулятивная кривая и кривая Лоренца?
49.Из каких основных элементов состоит статистическая таблица?
50.Чем статистическая таблица отличается от обычной таблицы?
51.Какие виды таблиц по характеру подлежащего вы знаете?
52.Классификация таблиц по строению сказуемого.
53.Что такое абсолютные величины, их виды и способы выражения?
54. Какой учет называется натуральным, условно-натуральным, трудовым и стоимостным?
55.Что такое относительные величины?
56.Виды относительных величин.
57. Сущность средней величины.
58. Как вычисляется средняя арифметическая простая?
59. В каких случаях применяется взвешенная средняя арифметическая?
60. Как вычисляется средняя интервального ряда?
61. Как вычисляется средняя из групповых или частных средних?
62. Особенности вычисления средней из относительных величин.
63. Свойства средней арифметической.
64. Средняя гармоническая и способы ее вычисления.
65. Средняя геометрическая и способы ее вычисления.
66. Средняя квадратическая, когда она применяется?
67. Мажорантность средних.
68. Что такое мода, когда и для чего она применяется и как вычисляется?
69. Отличие моды и средней величины.
70. Что такое медиана, когда и для чего она применяется?
71. Что такое вариации признака и каковы показатели вариации?
72. Основные свойства дисперсии.
73. Как определяется дисперсия альтернативного признака?
74. От каких факторов зависит общая вариация признака?
75. Что такое «правило сложения дисперсий», его сущность?
76. Что такое межгрупповая дисперсия и что она характеризует?
77. Что такое средняя из внутригрупповых дисперсий и ее назначение?
78. Что такое момент распределения, виды моментов и их назначение?
79. Что такое кривые распределения и их виды и характеристики?
80. Какими показателями характеризуется форма кривой распределения, и как они вычисляются?
81. Что такое моделирование ряда распределения?
82. Какие этапы моделирования вы знаете?
83. Что такое «степень свободы» - как понятие?
84. Критерии согласия, их виды, для чего они применяются?
85. Выборочное наблюдение: виды и способы, общие понятия.
86. Что такое «ошибка выборки» и почему применяется термин «средняя ошибка выборки»?
87. Что такое предельная ошибка и как она вычисляется?
88. Особенности вычисления предельных ошибок при различных видах и схемах отбора.
89. Почему ошибка типического отбора, как правило, меньше ошибки собственно-случайного отбора?
90. Как определяется необходимая численность выборки?
91. Функциональная и корреляционная связь: их особенности.
92. Простейшие методы установления тесноты связи.
93. В чем сущность балансового метода и дисперсионного анализа?
1. Что такое корреляционное отношение?
2. Каковы основные задачи корреляционного анализа?
3. Каковы задачи регрессионного анализа?
4. Каков экономический смысл коэффициентов регрессии?
5. Что такое коэффициент корреляции и как он вычисляется?
1. Что такое коэффициент детерминации?
2. Что такое множественная корреляция?
3. Сущность и методы вычисления частных коэффициентов.
4. Какие методы (кроме корреляционно-регрессионного анализа) вы еще знаете?
5. Что такое динамический ряд?
6. Какие приемы применяются для приведения рядов в сопоставимый вид?
Классификация динамических рядов.
Расчет средней динамического ряда.
Основные показатели, применяемые для анализа динамических рядов.
Что такое коэффициент опережения?
Важнейшие приемы обработки и анализа динамических рядов.
 2015-02-14
2015-02-14 9782
9782







