Скорость, ускорение, единицы их измерения

В математике скоростью изменения какой-либо функции f называется первая производная этой функции по времени:

.

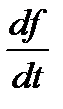Другое обозначение производной по времени, используемое еще со времен Ньютона, – точка над символом функции 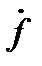. Производную по координате принято обозначать штрихом в качестве верхнего индекса: 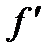. Если нужно указать, по какой именно координате берется производная, то соответствующую координату пишут в виде нижнего индекса: .

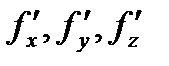В механике скоростью называют производную радиус-вектора (2) по времени. Обозначается скорость обычно латинской буквой 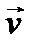(от латинского слова – скорость):

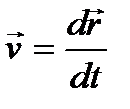. (3)

Такая скорость называется мгновенной скоростью. Мгновенная скорость – векторная величина. Направлен вектор скорости в ту же сторону, куда направлен вектор перемещения 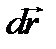. Единицей измерения скорости является метр-в-секунду (м/с).

Компоненты вектора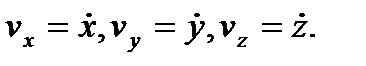

Средняя скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

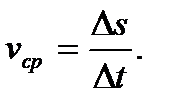(4)

Средняя скорость, в отличие от мгновенной скорости, величина скалярная. Для вычисления средней скорости нужно сложить все линии траектории, которую прошло тело, и разделить на прошедшее время. Например, на рис 4 Δs = s₁₃ + s₂₃ + s₃₂. Среднюю скорость нельзя вычислять как среднее арифметическое скоростей тела на отдельных участках пути. Средняя скорость равна среднему арифметическому от всех скоростей тела только в том случае, если тело двигалось с этими скоростями равные промежутки времени.

Иногда вводят в рассмотрение среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:

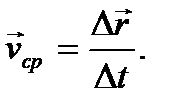(5)

В этом случае скорость (4) называют средней путевой скоростью, или средней скоростью по пройденному пути. На рис. 4 вектором перемещения будет являться вектор, соединяющий точки 1 и 3 (см. также рис. 5). Если в результате движения тело вернулось в исходную точку, то средняя скорость по перемещению будет равна нулю, а средняя путевая скорость будет отлична от нуля. Средняя путевая скорость будет равна нулю только в том случае, если тело вообще не двигалось с места.

Модуль вектора скорости вычисляется как производная пройденного пути по времени:

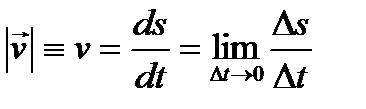. (6)

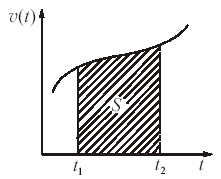
Рис. 6.

Пройденный путь как интеграл от скорости

Согласно (6), путь ds, пройденный за элементарный промежуток времени dt, равен ds = v(t)dt. Путь, пройденный телом за конечный промежуток времени от t₁ до t₂, находится интегрированием:

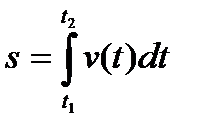
Пройденный путь численно равен площади криволинейной трапеции на графике зависимости скорости от времени (рис. 6).

Если модуль скорости не изменяется с течением времени, то движение называется равномерным. При равномерном движении скорость тела постоянна:

.

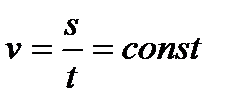Отсюда следует физический смысл скорости: скорость численно равна пути, пройденному за единицу времени.

Применяя понятие равномерного движения, можно сформулировать физический смысл мгновенной скорости: