1. Понятие о рядах динамики и их значение
Статистика изучает явления не только в статике, но и в динамике. Чтобы понять то или иное явление, правильно разобраться в нем, следует изучать его в динамике, то есть в движении, развитии.
Изучение явлений в их развитии достигается в статистике при помощи построения рядов динамики или динамических рядов (иногда их называют также временными или хронологическими рядами).
РЯДОМ ДИНАМИКИ в статистике называется ряд чисел, характеризующих изменение величины того или иного явления во времени.
В каждом ряду динамики имеются два основных элемента:
1) показатели времени t;
2) соответствующие им уровни развития изучаемого явления у.
В качестве показателей времени в рядах динамики выступают либо определенные даты (моменты) времени (например, начало или конец года, квартала и пр.), либо отдельные периоды (годы, кварталы, месяцы, сутки).
Ряды динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.
МОМЕНТНЫЕ ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики является следующая информация о списочной численности работников магазина:
| Дата | 1.01.96 | 1.04.96 | 1.07.96 | 1.10.96 | 1.01.97 |
| Число работников, чел. |
Посредством моментных рядов динамики в торговле изучают товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени.
ИНТЕРВАЛЬНЫЕ ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда динамики могут служить данные о товарообороте магазина в 1993 - 1997 гг.:
| Год | |||||
| Объем розничного товарооборота, тыс. руб. | 885,7 | 932,6 | 980,1 | 1028,7 | 1088,4 |
Посредством интервальных рядов динамики в торговле изучается изменение во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования (развития) изучаемых явлений за отдельные периоды.
Статистическое отображение развития изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. Ряды динамики с нарастающими итогами строятся, например, при определении общего объема товарооборота в розничной торговле. Так, объем продажи товаров в магазине определяется каждый месяц обобщением товарно-денежных отчетов за отдельные операционные периоды (пятидневки, недели, декады и т. д.).
ПРИМЕР: Воспользуемся данными о ходе реализации товаров в магазине за октябрь 1999 г. (графа 2).
| Пятидневки | Розничная реализация товаров, тыс.руб. | |
| За пятидневку | с начала месяца | |
| Первая | 5,2 | 5,2 |
| Вторая | 4,3 | 5,2+4,3=9,5 |
| Третья | 12,4 | 9,5+12.4=21,9 |
| Четвертая | 18,0 | 21,9+18,0=39,9 |
| Пятая | 21,9 | 39,9+21,9=61,8 |
| Шестая | 18,4 | 61,8+18,4=80,2 |
Данные графы 3 отображают обобщенные с начала месяца результаты продажи товаров по отдельным периодам работы предприятия в течение месяца.
2. Показатели, характеризующие тенденцию динамики
К показателям, характеризующим тенденцию динамики, относятся следующие:
• абсолютные приросты базисные (накопленные) и цепные (годовые);
• темпы роста (базисные и цепные);
• темпы прироста (базисные и цепные);
• абсолютное значение одного процента прироста;
• темп наращивания (изменения);
• средний темп прироста.
Рассмотрим некоторые из этих показателей.
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Базисный (накопленный) абсолютный прирост 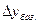 исчисляется как разность между сравниваемым уровнем
исчисляется как разность между сравниваемым уровнем 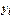 и уровнем, принятым за постоянную базу сравнения
и уровнем, принятым за постоянную базу сравнения 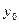 :
: 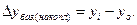
Цепной абсолютный прирост 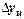 - разность между сравниваемым уровнем
- разность между сравниваемым уровнем 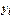 и уровнем, который ему предшествует,
и уровнем, который ему предшествует, 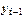 :
: 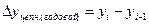
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Базисные темпы роста 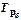 исчисляются делением сравниваемого уровня (
исчисляются делением сравниваемого уровня ( 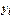 ) на уровень, принятый за постоянную базу сравнения,
) на уровень, принятый за постоянную базу сравнения, 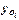 :
: 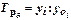
Цепные темпы роста 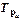 исчисляются делением сравниваемого уровня
исчисляются делением сравниваемого уровня 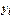 на предыдущий уровень
на предыдущий уровень 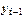 :
:
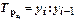
Если темп роста больше единицы (или 100%), это показывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Базисный темп прироста 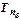 вычисляется делением сравниваемого базисного абсолютного прироста
вычисляется делением сравниваемого базисного абсолютного прироста 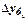 ,. на уровень, принятый за постоянную базу сравнения
,. на уровень, принятый за постоянную базу сравнения 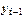 :
: 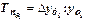
Цепной темп прироста 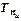 - это отношение сравниваемого цепного абсолютного прироста
- это отношение сравниваемого цепного абсолютного прироста 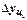 , к предыдущему уровню
, к предыдущему уровню 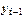 :
: 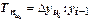 .
.
Темп наращивания (изменения) определяется путем деления абсолютного прироста (годового) 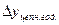 на уровень, принятый за постоянную базу сравнения
на уровень, принятый за постоянную базу сравнения 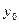 ; выражается в процентах:
; выражается в процентах: 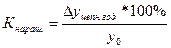
ПРИМЕР: Рассмотрим товарооборот магазина за 5 лет. Расчет показателей динамики приведен в таблице:
| Показатели | |||||
Товарооборот, тыс. руб. 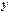 | 885,7 | 932,6 | 980,1 | 1028,7 | 1088,4 |
Абсолютный прирост, тыс. руб. Базисный 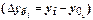 Цепной Цепной 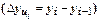 | - - | 932,6-885,7=46,9 932,6-885,7=46,9 | 980,1-885,7=94,4 980,1-932,6=47,5 | 143,0 48,6 | 202,7 59,7 |
Темп роста, % Базисный [ 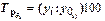 ] Цепной [ ] Цепной [ 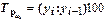 ] ] | - - | 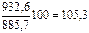 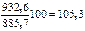 | 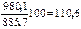 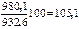 | 116,1 104,9 | 122,9 105,8 |
Темп прироста, % Базисный [ 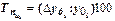 ] Цепной [ ] Цепной [ 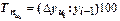 ] ] | - - | 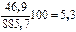 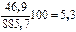 | 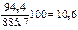 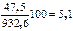 | 16,1 4,9 | 22,9 5,8 |
Темп наращивания, % [ 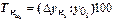 ] ] | - | 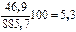 | 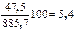 | 5,5 | 6,8 |
3. Средние показатели в рядах динамики
Для получения обобщающих показателей динамики социальных или экономических явлений определяются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста и пр.
Средний уровень показателя динамики характеризует типическую величину абсолютных уровней.
ПРИМЕР: Рассмотрим моментный динамический ряд. Товарные запасы в торговом предприятии на начало каждого месяца характеризуются следующими данными.
| Время | 01 января | 01 февраля | 01 марта | 01 апреля |
| Товарные запасы, млн. руб. |
Вычислим средние товарные запасы за I квартал. Определим сначала средние товарные запасы по месяцам. За январь они будут равны средней из данных на начало января и начало февраля, т.е. конец января.:
(120+140)/2= 130 млн. руб.
Соответственно за февраль (140 + 150) / 2 = 145 млн. руб.; март (150 + 160)/2= 155 млн. руб.
Таким образом, от моментного ряда можно перейти к интервальному:
| Время | январь | февраль | март |
| Товарные запасы, млн. руб. |
Теперь из среднемесячных показателей вычислим среднюю величину, т.е. средние товарные запасы за I квартал. Для расчета средней величины применим формулу средней арифметической простой:
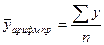 ; то есть (130 + 145 + 155)/3=430/3= 143,3 млн. руб.
; то есть (130 + 145 + 155)/3=430/3= 143,3 млн. руб.
На основании расчетов можно сделать вывод: для исчисления среднего уровня (средней величины) в интервальных рядах динамики применяется формула средней арифметической простой.
Вернемся к исходной информации, т.е. к моментному ряду динамики. Можно сразу исчислить среднюю величину или средние товарные запасы за I квартал, применив формулу средней хронологической из моментного ряда динамики:
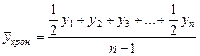 ,
,
где у - уровни ряда от первого до п -го момента времени;
п - число уровней ряда.
Таким образом, в I квартале 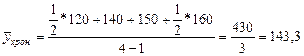 млн. руб.
млн. руб.
По формуле средней хронологической, имея данные о семи уровнях, можно исчислять средние уровни за полугодие; при наличии данных о тринадцати уровнях (на первое число каждого месяца) - за год.
На основании расчетов можно сделать вывод: для исчисления среднего уровня (средней величины) в моментных рядах динамики применяется формула средней хронологической.
Особенность этой формулы заключается в том, что первый и последний уровни ряда при суммировании берутся в половинном размере, а вся сумма делится на число уровней без одного. Объясняется это тем, что крайние уровни в моментном ряду относятся не только к характеризуемому периоду, но и к смежным. Средние уровни в моментных рядах динамики называются средними хронологическими, исчисленными за какие-то периоды.
В моментном ряду динамики с равностоящими датами времени средний уровень определяется по аналогичной формуле:
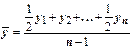 .
.
ПРИМЕР: Применение этой формулы проиллюстрируем на данных о списочной численности работников:
| Дата | 1.01.96 | 1.04.96 | 1.07.96 | 1.10.96 | 1.01.97 |
| Число работников, чел. |
При определении среднего уровня данного ряда динамики промежутки времени между отчетными датами практически принимаются за равновеликие. Тогда по формуле:
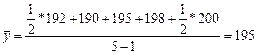 человек.
человек.
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле:
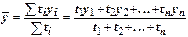 ,
,
где 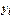 - уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени
- уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени 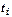 .
.
ПРИМЕР: Применение данной формулы проиллюстрируем на данных о состоянии численности работников магазина в апреле 1996 г. С 1 по 20 апреля в списочном составе работников магазина значилось 190 человек, с 21 апреля и до конца месяца числилось 196 человек. Тогда в соответствии с формулой для неравноотстоящих дат среднедневная (списочная) численность работников магазина в апреле составила:
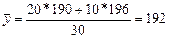 человека.
человека.
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста 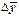 сумма цепных абсолютных приростов
сумма цепных абсолютных приростов 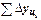 делится на их число n:
делится на их число n:
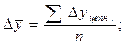
Применение формулы расчета среднего абсолютного прироста 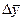 проиллюстрируем на данных таблицы о цепных абсолютных приростах товарооборота магазина (см. выше):
проиллюстрируем на данных таблицы о цепных абсолютных приростах товарооборота магазина (см. выше):
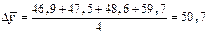 тыс.руб.
тыс.руб.
Средний темп роста - обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста 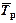 применяется формула
применяется формула
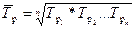
где 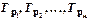 , - индивидуальные (цепные) темпы роста (в коэффициентах), n - число индивидуальных темпов роста.
, - индивидуальные (цепные) темпы роста (в коэффициентах), n - число индивидуальных темпов роста.
Применение формулы расчета средних темпов роста проиллюстрируем на данных таблицы о цепных темпах роста розничного товарооборота магазина, заменив процентное их выражение коэффициентами: 1993 г.- 1,053; 1994 г. - 1,051 и т.д.
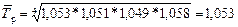 или 105,3%
или 105,3%
Средний темп прироста 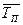 можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста
можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста 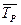 для получения средних темпов прироста
для получения средних темпов прироста 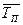 используется зависимость:
используется зависимость:

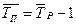 (при выражении среднего темпа роста в коэффициентах).
(при выражении среднего темпа роста в коэффициентах).
Применяя эту формулу, можно вычислить средний темп прироста розничного товарооборота магазина за 1993-1997 гг. (по той же таблице) на основе среднего темпа роста:
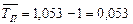 или 5,3 %.
или 5,3 %.
4. Абсолютное значение одного процента прироста
Абсолютное значение одного процента прироста (изменения) представляет собой отношение цепного годового (месячного, квартального) абсолютного прироста (изменения) к цепному годовому (месячному, квартальному) темпу прироста и показывает, какая абсолютная величина скрывается за одним процентом прироста; выражается в абсолютных единицах измерения:
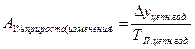 или
или 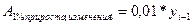 .
.
...
 2015-02-15
2015-02-15 1978
1978
