Политропические процессы

Рассмотренные выше изотермический и адиабатический процессы изменения состояния газа являются идеализированными процессами: первый из них требует идеального контакта с окружающей средой или с термостатом, второй – столь же идеальной изоляции. Оба эти процесса можно рассматривать как частные крайние случаи более общего процесса, называемого политропическим. Так называется всякий процесс изменения состояния, при котором теплоемкость C остается постоянной и равной

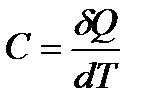, или δQ = CdT.

Кривая, изображающая политропический процесс, называется политропой. Если обозначить молярную теплоемкость идеального газа в политропическом процессе через C, то уравнение политропы записывается как pVⁿ = const или TV^n–1 = const,

где

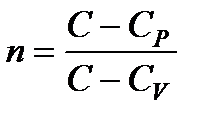. (124)

Постоянная n называется показателем политропы.

Для изотермического процесса C = ∞. Подставляя это значение в уравнение (124), получаем n = 1. Согласно уравнению TV^n–1 = const получаем T = const.

Для адиабатического процесса C = 0. Согласно (124) 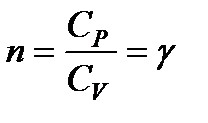. Тогда уравнение pVⁿ = const превращается в уравнение адиабаты pV^γ = const.

Теплоемкости реальных газов зависят от состояния. Однако у идеального газа теплоемкости те зависят от состояния. Поэтому можно вычислить показатель политропы для изобарического и изохорического процессов.

Для изобарического процесса C = C_P и n = 0. Согласно уравнению pVⁿ = const получаем P = const.

Для изохорического процесса C = C_V и n = ∞. Вычислим из уравнения PVⁿ = const корень n –й степени 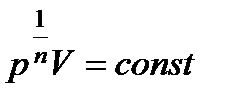и подставим значение n = ∞. Тогда получим V = const.