Перевод уравнения прямой из общего вида в канонический

Пусть прямая 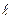задана в общем виде: 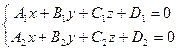для того, чтобы перевести ее в канонический вид, возьмем две точки принадлежащие данной прямой, т.е. два частных решения данной системы. Для получения частного решения системы, проще всего одной из переменных дать произвольное значение, например, 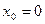. Подставить это значение в систему и решить полученную систему с двумя переменными: 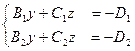, например, по правилу Крамера:

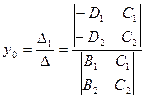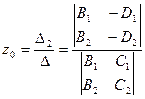, , найдена точка 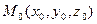. Если же определитель 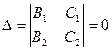, то необходимо другой переменной дать произвольное значение, например, 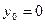и решить систему относительно х и z.Аналогично найти еще одно частное решение системы 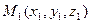. И записать уравнение прямой по двум точкам: .

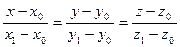Перевод уравнения прямой из канонического вида в общий

Пусть дана прямая 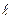в каноническом виде: 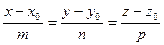. Для того, чтобы ее перевести в общий вид, приравняем попарно отношения (при условии, что 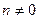): 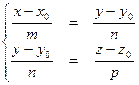после преобразований получим: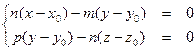

Прямая 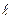получена в общем виде, как пересечение двух плоскостей. Если же n=0. то можно получить одну из плоскостей, приравняв первое отношение к третьему.