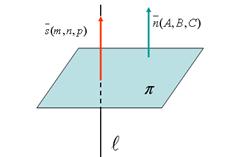
Пусть плоскость 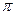 задана своим общим уравнением: Ax+By+Cz+D=0, а прямая
задана своим общим уравнением: Ax+By+Cz+D=0, а прямая 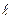 в каноническом виде:
в каноническом виде: 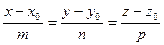 . Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.
. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.
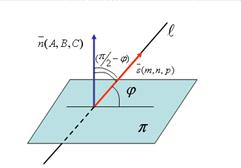 Обозначим через
Обозначим через 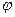 угол между прямой
угол между прямой 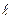 и плоскостью
и плоскостью 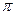 . Тогда угол между нормалью к плоскости вектором
. Тогда угол между нормалью к плоскости вектором 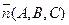 и направляющим вектором прямой
и направляющим вектором прямой 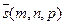 будет равен
будет равен 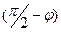 .
.
Тогда sin 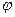 =cos
=cos 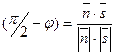 . Так как угол
. Так как угол 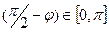 , то синус острого угла между прямой
, то синус острого угла между прямой 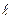 и плоскостью
и плоскостью 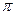 можно найти по формуле:
можно найти по формуле: 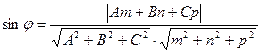
Условие параллельности прямой 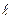 и плоскости
и плоскости 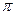
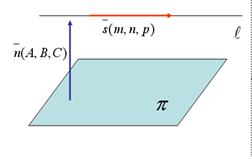 Если прямая
Если прямая 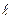 параллельна плоскости
параллельна плоскости 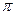 , то векторы
, то векторы 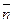 и
и 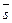 перпендикулярны, т.е. их скалярное произведение равно 0.
перпендикулярны, т.е. их скалярное произведение равно 0. 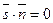 , т.е. в координатной форме: Am+Bn+Cp=0.
, т.е. в координатной форме: Am+Bn+Cp=0.
Условие перпендикулярности прямой 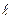 и плоскости
и плоскости 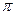
 Если прямая
Если прямая 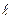 перпендикулярна плоскости
перпендикулярна плоскости 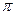 , то векторы
, то векторы 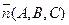 и
и 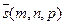 параллельны, т.е. должно быть выполнено равенство:
параллельны, т.е. должно быть выполнено равенство: 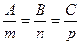
 2015-02-18
2015-02-18 675
675








