Считая, что сила, действующая на частицу, пропорциональна смещению х и направлена противоположно смещению, в положении равновесия 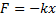 . Рассматривая одномерное движение запишем уравнение II-го закона Ньютона:
. Рассматривая одномерное движение запишем уравнение II-го закона Ньютона: 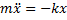 , или, вводя параметр
, или, вводя параметр 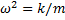 , имеем:
, имеем:
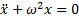 (1)
(1)
Уравнение (1) называется уравнением свободных линейных колебаний. Решение такого уравнения ищется в классе периодических функций sin, cos. После подстановки в уравнение функций вида: 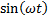 ,
, 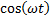 а также линейных комбинаций таких функций, получаем, что общим решением уравнения (1) является выражение вида:
а также линейных комбинаций таких функций, получаем, что общим решением уравнения (1) является выражение вида:
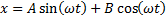 (2)
(2)
где A, B=const, определяются из начальных данных. Как известно, точное решение дифференциального уравнения второго порядка требует задания двух значений 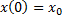 и
и 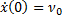 – значения координаты и скорости в начальный момент времени. Подстановка
– значения координаты и скорости в начальный момент времени. Подстановка 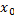 ,
, 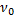 в решение (2) позволяет определить для константы А,В. Действительно:
в решение (2) позволяет определить для константы А,В. Действительно:
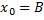 ,
, 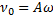 .
.
 2015-02-18
2015-02-18 1179
1179
