2014-02-04
3198
Переход от системы уравнений в форме (2.1) к уравнениям состояния может быть осуществлён различными путями. Одной и той же исходной системе уравнений может соответствовать несколько систем в форме Коши в зависимости от способа определения переменных состояния. Рассмотрим наиболее распространённые подходы.
Способ 1. Пусть объект управления описывается линейными дифференциальными уравнениями с постоянными коэффициентами, которые можно представить в виде
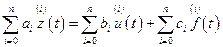, (2.3)`
где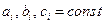 
, 
.
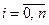Запишем дифференциал с помощью s-оператора Лапласа при нулевых начальных условиях, приняв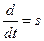 
.
Тогда уравнение (2.3)` в операторной форме примет вид:
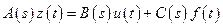, (2.4)
где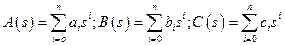 
.
Определим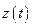 
из формулы (2.4):
, (2.4)`
где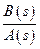 
и 
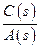называются операторами объекта по управлению и возмущению соответственно.
Разложим операторы объекта на элементарные слагаемые
; 
, (2.5)
где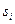 
- корни характеристического уравнения
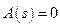; (2.6)
; 
; 
; 
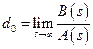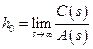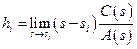. (2.7)
С учётом (2.5) уравнение (2.4) можно записать в виде:
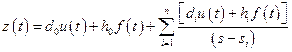. (2.8)
Введём переменные состояния
. (2.8)`
Тогда уравнение (2.2) можно записать следующим образом:
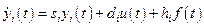, (2.9)
а уравнение (2.8) примет вид:
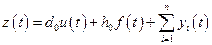. (2.10)
Уравнения (2.9) и (2.10) называются уравнениями состояния линейного стационарного объекта.
Уравнения состояния (2.9) и (2.10) удобно переписать в матрично-векторной форме
; 
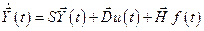, (2.11)
где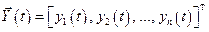 
;
;
;
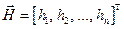- символ транспонирования;
- диагональная матрица, элементы главной диагонали которой равны корням характеристического уравнения (2.6), а остальные элементы – нули;
- 
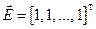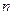-мерный вектор.
Недостатком этого способа является необходимость решать характеристическое уравнение (2.6), что усложняется при больших значениях полинома.
Этот недостаток устраняется, используя способ 2.
БИЛЕТ 7) Способ 2 может использоваться, если дифференциальные уравнения (2.1) также являются линейными с постоянными коэффициентами.
Пусть для простоты предположим, что возмущения отсутствуют, т.е.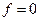 
.
Введём вектор 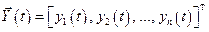, компоненты которого определяются следующим образом: 
; 
; …; 
.
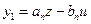Тогда уравнения состояния (2.9) и (2.10) можно записать в виде
; 
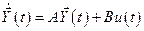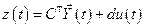, (2.12)
где A - квадратичная n -мерная матрица;
B и C - n -мерные векторы;
; 
; 
; 
.
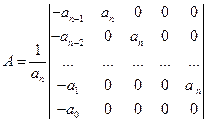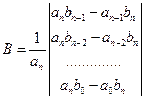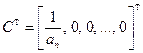Способ 3 применяется, если дифференциальный оператор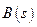 
имеет порядок меньше, чем 
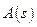, т.е. 
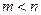(производная 
имеет порядок больше, чем производная 
).
Пусть возмущения отсутствуют, т.е. .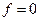
Тогда уравнение (2.4) можно переписать в виде:
.
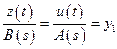Откуда видно, что
, 
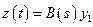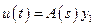, (2.13)
где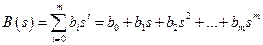 
; 
.
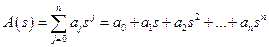С учётом этого получаем, что
; 
. (2.14)
Введём переменные состояния 
; 
; 
; 
; 
.
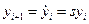С учётом этого выражения (2.14) можно переписать в виде:
;
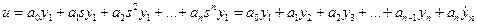. (2.14)`
В матричных обозначениях уравнение состояния приобретёт вид:
; 
.
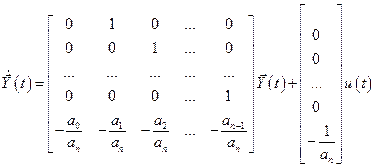Здесь 
.
Способ 4. Часто свойства ОУ изменяются со временем. Если объект линеен, то нестационарность проявляется в зависимости коэффициентов от времени.
Пусть возмущения отсутствуют (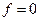). Тогда уравнение (2.1) можно записать в виде (см. (2.3)`):
(2.15)
По аналогии со способом 1 уравнения состояния (2.11), можно представить следующим образом:
; 
, (2.16)
где 
; 
; (2.17)
; 
.
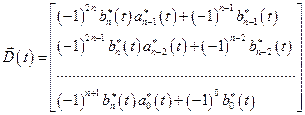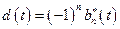В свою очередь
; 
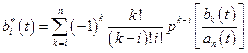. (2.18)
Способ 5 может использоваться, если нелинейные уравнения не содержат производной от управляющего воздействия 
.
Пусть возмущения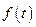 
отсутствуют, и объект описывается уравнением
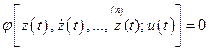, (2.19)
которое можно разрешить относительно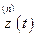 
. Тогда
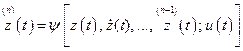. (2.20)
Введём переменные состояния
;
;
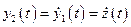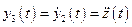; (2.21)
…
;
.
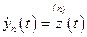С учётом введенных переменных состояния 
уравнение (1.20) примет следующий вид:
. (2.22)
Уравнения (2.21) и (2.22) представляют собой уравнения состояния для случая (2.19)
Уравнения состояния в векторной форме можно записать в виде
; 
, (2.23)
где .
Способ 6. Рассмотренные методы получения уравнений состояния могут быть применены и к многомерным объектам, для которых 
представляет собой 
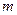-мерный вектор управлений с компонентами 
, 
, …, 
.
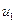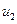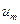Для многомерных объектов, как и для одномерных объектов, уравнения состояния имеют вид:
; 
, (2.24)
где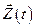 
- 
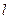-мерный вектор управляемых процессов с компонентами 
, 
, …, 
;
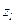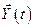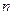- -мерный вектор состояния с компонентами 
, 
, …, 
.
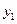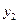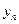Явная зависимость функци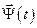й 
и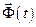 
от времени 
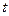указывает на то, что к объекту, кроме управляющего воздействия , приложено и внешнее воздействие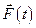 
(см. рис. 2.1).
Объекты, у которых в уравнениях состояния есть явная зависимость от времени 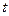, называются неавтономными. Если в уравнениях состояния нет явной зависимости от времени 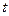, то такие объекты называются автономными.
Способ 7. Методы описания непрерывных объектов приемлемы и для дискретных объектов, которые описываются не дифференциальными, а разностными уравнениями, связывающими друг с другом выходные и входные процессы в различные дискретные моменты времени. Для одномерного дискретного объекта, разностные уравнения можно записать в форме
,
где 
.
Это уравнение можно заменить на 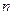разностных уравнений первого порядка.
В результате математическое описание многомерного дискретного объекта в векторной форме сводится к системе уравнений состояния, аналогичных уравнениям (2.24):
; 
. (2.25)
